當(dāng)前位置：試卷中心 > 試卷詳情

2023年山東省濟(jì)寧市微山縣中考數(shù)學(xué)一模試卷

發(fā)布：2024/4/20 14:35:0

一、選擇題：本大題共10小題，每題3分，共30分．在每小題給出的四個選項中，只有一項符合題目要求．

1．在-3，2，-6，0四個數(shù)中，最小的數(shù)是（　　）
A．-3 B．2 C．-6 D．0
組卷：93引用：3難度：0.9
解析
2．下列四幅圖案中，既是軸對稱圖形又是中心對稱圖形的是（　　）
A． B． C． D．
組卷：37引用：2難度：0.9
解析
3．數(shù)據(jù)0.00519用科學(xué)記數(shù)法表示為（　　）
A．5.19×10^-2 B．5.19×10^-3 C．5.19×10^-4 D．5.19×10^-5
組卷：54引用：3難度：0.9
解析
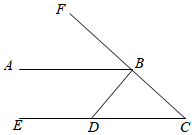4．如圖，AB∥CD，BD⊥CF，垂足為B，∠ABF=35°，則∠BDC的度數(shù)為（　　）
A．25° B．35° C．45° D．55°
組卷：262引用：3難度：0.5
解析
5．不等式組
3
（
x
-
1
）
＜
2
x
-
2
x
+
3
≥
1
，的解集在數(shù)軸上表示正確的是（　　）
A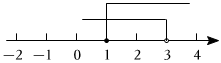． B．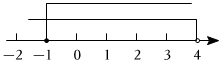
C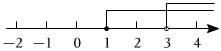． D．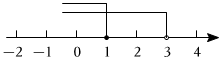
組卷：202引用：4難度：0.7
解析
6．分式
x
-
2
x
-
1
÷
（
3
x
-
1
-
x
-
1
）
化簡結(jié)果是（　　）
A．
-
1
x
+
2
B．
1
x
+
2
C．
-
1
x
-
2
D．
1
x
-
2
組卷：442引用：2難度：0.8
解析
7．現(xiàn)規(guī)定：a^*b=a²-ab+b,例如2*1=2²-2×1+1=3，則方程x*2=0的根的情況為（　　）
A．有兩個不相等的實數(shù)根 B．有兩個相等的實數(shù)根
C．沒有實數(shù)根 D．必有一個正數(shù)根
組卷：178引用：6難度：0.6
解析

當(dāng)前模式為游客模式，立即登錄查看試卷全部內(nèi)容及下載

三、解答題：本大題共7題，滿分0分．解答應(yīng)寫出文字說明、證明過程或推演過程．

21．閱讀材料：一般地，若a^x=N（a＞0，a≠1），則x叫做以a為底N的對數(shù)，記作：x=log_aN．比如指數(shù)式2⁴=16可以轉(zhuǎn)化為4=log₂16，對數(shù)式2=log₅25可以轉(zhuǎn)化為5²=25．我們根據(jù)對數(shù)的定義可得到對數(shù)的一個性質(zhì)：log_a（M?N）=log_aM+log_aN（a＞0，a≠1，M＞0，N＞0）；理由如下：設(shè)log_aM=m,log_aN=n,則M=a^m，N=aⁿ，∴M?N=a^m?aⁿ=a^m+n，由對數(shù)的定義得m+n=log_a（M?N）．又∵m+n=log_aM+log_aN，∴l(xiāng)og_a（M?N）=log_aM+log_aN．
解決問題：（1）將指數(shù)4³=64轉(zhuǎn)化為對數(shù)式
；
（2）證明
lo
g
a
M
N
=
lo
g
a
M
-
lo
g
a
N
（
a
＞
0
，
a
≠
1
，
M
＞
0
，
N
＞
0
）
；
拓展運(yùn)用：（3）計算：log₃2+log₃6-log₃4．
組卷：591引用：3難度：0.6
解析
22．在平面直角坐標(biāo)系中，拋物線y=mx²-4mx+4m+6（m＜0）與x軸交于A，B兩點（點A在點B的左側(cè)），與y軸交于點C，頂點為點D．

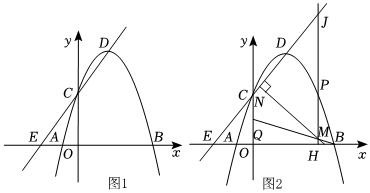
（1）當(dāng)m=-6時，直接寫出點A，C，D的坐標(biāo)；
（2）如圖1，直線DC交x軸于點E，若
tan
∠
BED
=
4
3
，求m的值及直線DE的解析式；
（3）如圖2，在（2）的條件下，若點Q為OC的中點，連接BQ，動點P在第一象限的拋物線上運(yùn)動，過點P作x軸的垂線．垂足為H，交BQ于點M，交直線ED于點J，過點M作MN⊥DE，垂足為N．是否存在PM與MN和的最大值？若存在，求出PM與MN和的最大值；若不存在，請說明理由．
組卷：173引用：2難度：0.1
解析