2022-2023學年四川省成都市樹德中學光華校區(qū)高一（下）期末數(shù)學模擬試卷（1）

一、單選題（共40分）

• 1．已知向量

  a

  =（1，0），

  b

  =（1，1），若

  a

  +λ

  b

  與λ

  a

  +

  b

  共線，則實數(shù)λ的值為（　　）

  A．-1

  B．1

  C．±1

  D．0
  組卷：277引用：5難度：0.7

  解析

• 2．將正弦函數(shù)f（x）=sinx的圖象先向左平移

  π

  3

  個單位長度，再將得到的圖象上所有點的橫坐標縮短到原來的

  1

  2

  ，縱坐標不變，最后得到函數(shù)g（x）的圖象，則g（x）=（　　）

  A． g （ x ） = sin （ 2 x + 2 π 3 ）	B． g （ x ） = sin （ 2 x + π 3 ）
  C． g （ x ） = sin （ x 2 + π 3 ）	D． g （ x ） = sin （ x 2 + π 6 ）
  組卷：847引用：7難度：0.9

  解析

• 3．在△ABC中，角A，B，C所對的邊分別為a,b,c.已知a=

  2

  ，b=

  3

  ，

  B

  =

  π

  3

  ，則角A為（　　）

  A． 3 π 4

  B． π 3

  C． π 4

  D． π 4 或 3 π 4
  組卷：360引用：6難度：0.7

  解析

• 4．已知α，β是兩個不重合的平面，m,n是兩條不同的直線，則下列命題正確的是（　　）

  A．若m⊥α，n⊥β，m⊥n,則α⊥β	B．若m∥α，n∥β，m∥n,則α∥β
  C．若m∥α，n?β，α∥β，則m∥n	D．若m∥α，n∥β，α⊥β，則m⊥n
  組卷：189引用：5難度：0.6

  解析

• 5．在四面體ABCD中，AB=CD，且異面直線AB與CD所成的角為70°，M，N分別是邊BC，AD的中點，則異面直線MN和AB所成的角為（　　）

  A．35°

  B．55°

  C．35°或55°

  D．20°或70°
  組卷：102引用：2難度：0.7

  解析

• 6．已知等邊三角形SAB為圓錐的軸截面，AB為圓錐的底面直徑，O，C分別是AB，SB的中點，過OC且與平面SAB垂直的平面記為α，若點S到平面α的距離為

  6

  ，則該圓錐的側面積為（　　）

  A．8π

  B．16π

  C．24π

  D．32π
  組卷：121引用：3難度：0.6

  解析

• 7．已知正方體ABCD-A₁B₁C₁D₁的棱長為1，E為DD₁中點，F(xiàn)為棱CD上異于端點的動點，若平面BEF截該正方體所得的截面為四邊形，則線段CF的取值范圍是（　　）

  A．（ 1 3 ，1）

  B．（ 1 2 ，1）

  C．[ 1 2 ， 2 3 ）

  D．（0， 1 2 ]
  組卷：92引用：4難度：0.6

  解析

四、解答題（共70分）

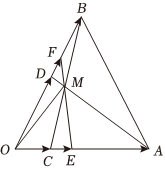• 21．如圖所示，在△ABO中，

  OC

  =

  1

  4

  OA

  ，

  OD

  =

  1

  2

  OB

  ，AD與BC相交于點M，設

  OA

  =

  a

  ，

  OB

  =

  b

  ．
  （1）試用向量

  a

  ，

  b

  表示

  OM

  ；
  （2）過點M作直線EF分別交線段AC，BD于點E，F(xiàn)，記

  OE

  =

  λ

  OA

  ，

  OF

  =

  μ

  OB

  ，求證：不論點E，F(xiàn)在線段AC，BD上如何移動，

  1

  λ

  +

  3

  μ

  為定值．
  組卷：435引用：8難度：0.7

  解析

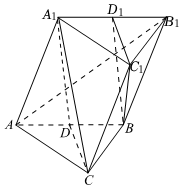• 22．如圖，在斜三棱柱ABC-A₁B₁C₁中，AC=BC，D為AB的中點，D₁為A₁B₁的中點，平面A₁B₁C₁⊥平面ABB₁A₁，異面直線BC₁與AB₁互相垂直．
  （1）求證：平面A₁DC∥平面BD₁C₁；
  （2）若CC₁與平面ABB₁A₁的距離為x,A₁C=AB₁=6，三棱錐A₁-ACD的體積為y,試寫出y關于x的函數(shù)關系式；
  （3）在（2）的條件下，當CC₁與平面ABB₁A₁的距離為多少時，三棱錐A₁-ACD的體積取得最大值？并求出最大值．
  組卷：471引用：4難度：0.3

  解析