2022-2023學年安徽省六安市毛坦廠中學東部新城校區高一（下）期中數學試卷

一、選擇題：本題共8小題，每小題5分，共40分。在每小題給出的四個選項中，只有一項是符合題目要求的。

• 1．已知復數z=m（m-1）+mi為純虛數，則實數m的值為（　　）

  A．-1

  B．1

  C．1或-1

  D．-1或0
  組卷：65引用：7難度：0.8

  解析

• 2．設集合A={x|x-2≥0}，B={x|x²-2x-8＜0}，全集U=R，則B∪?_UA=（　　）

  A．（4，+∞）

  B．（-∞，4）

  C．[4，+∞）

  D．（-∞，-4]
  組卷：135引用：5難度：0.7

  解析

• 3．已知tanα=2，則

  6

  sinα

  +

  cosα

  3

  sinα

  -

  2

  cosα

  的值為（　　）

  A．-4

  B． 13 4

  C． - 13 4

  D． ± 13 4
  組卷：480引用：3難度：0.9

  解析

• 4．下列說法錯誤的是（　　）

  A．球體是旋轉體

  B．圓柱的母線平行于軸

  C．斜棱柱的側面中沒有矩形

  D．用平面截正棱錐所得的棱臺叫做正棱臺
  組卷：118引用：8難度：0.6

  解析

• 5．方程x+lgx=3的解所在區間是（　　）

  A．（0，1）

  B．（1，2）

  C．（2，3）

  D．（0，2）
  組卷：89引用：3難度：0.9

  解析

• 6．若a＜0，則a+

  1

  a

  （　　）

  A．有最小值2

  B．有最大值2

  C．有最小值-2

  D．有最大值-2
  組卷：91引用：10難度：0.9

  解析

• 7．在△ABC中，內角A、B、C的對邊長分別為a、b、c,已知

  3

  cos

  A

  cos

  C

  =

  a

  c

  ，且a²-c²=2b,則b=（　　）

  A．4

  B．3

  C．2

  D．1
  組卷：434引用：7難度：0.9

  解析

四、解答題：本題共6小題，共70分。解答應寫出文字說明、證明過程或演算步驟。

• 21．對于定義在D上的函數f（x），如果存在實數x₀，使得f（x₀）=x₀，那么稱x₀是函數f（x）的一個不動點．已知函數

  f

  （

  x

  ）

  =

  lo

  g

  2

  [

  a

  ?

  4

  x

  -

  1

  2

  -

  （

  a

  -

  1

  ）

  2

  x

  -

  1

  +

  a

  2

  +

  1

  4

  ]

  ．
  （1）若a=0，求f（x）的不動點；
  （2）若函數f（x）恰有兩個不動點x₁，x₂，且0＜x₁＜x₂，求正數a的取值范圍．
  組卷：43引用：4難度：0.5

  解析

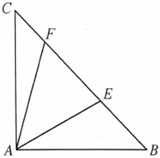• 22．如圖，某小區有一塊空地△ABC，其中AB=50，AC=50，∠BAC=90°，小區物業擬在中間挖一個小池塘△AEF，E，F在邊BC上（E，F不與B，C重合，且E在B，F之間），且

  ∠

  EAF

  =

  π

  4

  ．
  （1）若

  BE

  =

  10

  2

  ，求EF的值；
  （2）為節省投入資金，小池塘△AEF的面積需要盡可能的小．設∠EAB=θ，試確定θ的值，使得△AEF的面積取得最小值，并求出△AEF面積的最小值．
  組卷：613引用：9難度：0.3

  解析