2021-2022學年江西省宜春實驗中學高二（下）開學數學試卷（文科）

一、選擇題：本大題共12小題，每小題5分，共60分.在每小題給出的四個選項中，只有一個項是符合題目要求的.

• 1．已知雙曲線的焦點在y軸上，其漸近線與直線y=±2x垂直，則其離心率為（　　）

  A． 5

  B． 5 5

  C． 5 2

  D． 2 5 5
  組卷：2引用：1難度：0.7

  解析

• 2．命題“?x₀∈R，

  2

  x

  0

  ≤

  x

  2

  0

  ”的否定是（　　）

  A．不存在x0∈R， 2 x 0 ＞ x 2 0	B．?x0∈R， 2 x 0 ＞ x 2 0
  C．?x∈R，2x≤x2	D．?x∈R，2x＞x2
  組卷：125引用：8難度：0.9

  解析

• 3．擲一枚均勻的硬幣兩次，事件M={一次正面向上，一次反面向上}；事件N={至少一次正面向上}．下列結果正確的是（　　）

  A．P（M）= 1 3 ，P（N）= 1 2	B．P（M）= 1 2 ，P（N）= 3 4
  C．P（M）= 1 3 ，P（N）= 3 4	D．P（M）= 1 2 ，P（N）= 1 2
  組卷：88引用：1難度：0.7

  解析

• 4．閱讀如圖的程序框圖，運行相應的程序，輸出S的值為（　　）
  

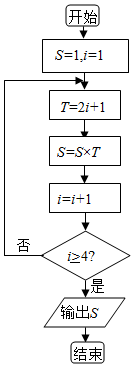
  A．15

  B．105

  C．245

  D．945
  組卷：537引用：43難度：0.9

  解析

• 5．已知F₁、F₂是橢圓的兩個焦點，滿足

  M

  F

  1

  ?

  M

  F

  2

  =0的點M總在橢圓內部，則橢圓離心率的取值范圍是（　　）

  A．（0，1）

  B．（0， 1 2 ]

  C．（0， 2 2 ）

  D．[ 2 2 ，1）
  組卷：2774引用：99難度：0.7

  解析

• 6．設P為曲線C：y=x²+2x+3上的點，且曲線C在點P處切線傾斜角的取值范圍是

  [

  0

  ，

  π

  4

  ]

  ，則點P橫坐標的取值范圍是（　　）

  A． [ - 1 ，- 1 2 ]

  B．[-1，0]

  C．[0，1]

  D．[ 1 2 ，1]
  組卷：1997引用：86難度：0.9

  解析

• 7．在正方形ABCD內任取一點P，則使∠APB＜90°的概率是（　　）

  A． π 8

  B． π 4

  C． 1 - π 8

  D． 1 - π 4
  組卷：41引用：5難度：0.7

  解析

三、計算題：本大題共6小題，共70分.解答應寫出必要的文字說明、證明過程或演算步驟.

• 21．設函數f（x）=[ax²-（4a+1）x+4a+3]e^x．
  （Ⅰ）若曲線y=f（x）在點（1，f（1））處的切線與x軸平行，求a；
  （Ⅱ）若f（x）在x=2處取得極小值，求a的取值范圍．
  組卷：6569引用：14難度：0.3

  解析

• 22．已知雙曲線的中心在原點，焦點F₁、F₂在坐標軸上，離心率為

  2

  ，且過點（4，-

  10

  ）．
  （1）求雙曲線方程；
  （2）若點M（3，m）在雙曲線上，求證：點M在以F₁F₂為直徑的圓上；
  （3）在（2）的條件下求△F₁MF₂的面積．
  組卷：399引用：6難度：0.3

  解析