2023年陜西省西安交大附中中考數學四模試卷

一、選擇題（共8小題，每小題3分，計24分。每小題只有一-個選項是符合題意的）

• 1．計算：-5-（-3）=（　　）

  A．8

  B．2

  C．-2

  D．-8
  組卷：137引用：2難度：0.8

  解析

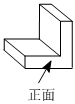• 2．如圖所示的幾何體的左視圖是（　　）

  A．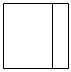

  B．

  C．

  D．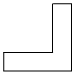
  組卷：59引用：2難度：0.8

  解析

• 3．下列計算結果為a⁶的是（　　）

  A．a3+a3

  B．（3a）2

  C．a12÷a2

  D．a5?a
  組卷：49引用：2難度：0.7

  解析

• 4．某班學生對三角形內角和為180°展開證明討論，以下四個學生的作法中，不能證明△ABC的內角和為180°的是（　　）

  A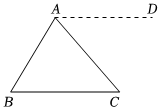． 過點A作AD∥BC

  B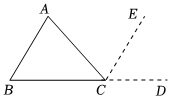． 延長BC到點D，過點C作CE∥AB

  C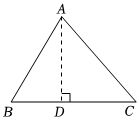． 過點A作AD⊥BC于點D

  D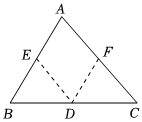． 過BC上一點D作DE∥AC，DF∥AB
  組卷：82引用：2難度：0.5

  解析

• 5．若直線l：y=kx+b經過點（0，y₁），（x₂，y₂），且x₂＞0時，y₂＜y₁＜0，則直線l不可能經過的點是（　　）

  A．（-2，-1）

  B．（2，-1）

  C．（2，1）

  D．（-2，1）
  組卷：270引用：2難度：0.7

  解析

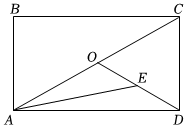• 6．如圖，在矩形ABCD中，AB=4，AD=6，O，E分別為AC，OD的中點，連接AE，則△AED的面積為（　　）

  A．3

  B．6

  C．9

  D．12
  組卷：290引用：2難度：0.7

  解析

• 7．如圖，△ACB內接于⊙O，AB是⊙O的直徑，點E是圓上一點，連接OE，CE，BE，

  ?

  BC

  =2

  ?

  BE

  ，∠CBA=48°，則∠CBE的度數為（　　）

  A．107°

  B．110°

  C．117°

  D．120°
  組卷：275引用：2難度：0.6

  解析

• 8．已知拋物線y=-x²+2ax+c（a＞0）的頂點到x軸的距離為9，拋物線與x軸交點之間的距離為6a,則a的值為（　　）

  A．1

  B．2

  C．3

  D．4
  組卷：420引用：2難度：0.5

  解析

三、解答題（共13小題，計81分。解答應寫出過程）

• 25．已知拋物線y=x²-6x+c與x軸交于點A，B（點A在點B的左側），與y軸交于點C（0，5）．
  （1）求拋物線的表達式及頂點坐標；
  （2）將拋物線沿y軸方向向上平移k個單位（k＞0）．平移后拋物線的頂點為點P，且點P在x軸下方，是否存在點P，使得以B，C，P為頂點的三角形為直角三角形？若存在，求出k的值；若不存在，請說明理由．
  組卷：468引用：2難度：0.5

  解析

• 26．問題提出
  （1）如圖①，在Rt△ABC中，BC=6，點D為斜邊AC的中點，且BD=5，求tan∠DBC的值；
  問題解決
  （2）如圖②，現有一塊邊長為1米的正方形鋼板ABCD，其中∠B，∠C，∠D均有不同程度的磨損，不能使用，王師傅計劃過點A裁出一個形如四邊形AEGF的零件，其中點F，G，E分別在邊AB，BC，CD上，且點F為AB的中點．
  ①王師傅想要使得∠FGE=90°，在手頭沒有直角尺的情況下，進行如下操作：
  第一步：取一根筆直的木棒，用鉛筆在木棒上任意點出M，N兩點；
  第二步：將木棒斜放在鋼板上，使點M與點F重合，保持點N不動，將木棒進行旋轉，使點M落在BC上，在鋼板上將點M對應的位置標記為點G；
  第三步：將FN延長，再將木棒繞點N旋轉，使點M落在FN的延長線上，記點M的對應點為點Q；
  第四步：作射線GQ交DC于點E，則∠FGE=90°．
  請問，王師傅的操作方法是否能夠得到∠FGE=90°？請證明．
  ②在①的條件下，王師傅想要得到最大面積的四邊形AEGF，請你計算四邊形AEGF面積的最大值．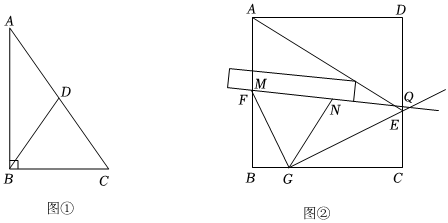
  
  組卷：299引用：2難度：0.4

  解析