2022-2023學年遼寧省錦州市高二（上）期末數學試卷

一、選擇題：本題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的．

• 1．直線x+y-3=0的傾斜角是（　　）

  A．30°

  B．45°

  C．135°

  D．150°
  組卷：71引用：3難度：0.9

  解析

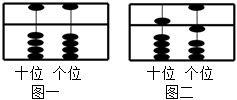• 2．算盤是中國古代的一項重要發明，迄今已有2600多年的歷史．現有一算盤，取其兩檔（如圖一），自右向左分別表示十進制數的個位和十位，中間一道橫梁把算珠分為上下兩部分，梁上一珠撥下，記作數字5，梁下四珠，上撥一珠記作數字1（如圖二算盤表示整數51）．若撥動圖1的兩枚算珠，則可以表示不同整數的個數為（　　）

  A．6

  B．8

  C．10

  D．15
  組卷：90引用：3難度：0.7

  解析

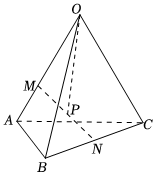• 3．如圖，在四面體OABC中，M是棱OA上靠近點A的三等分點，N，P分別是BC，MN的中點．設

  OA

  =

  a

  ，

  OB

  =

  b

  ，

  OC

  =

  c

  ，則向量

  OP

  可表示為（　　）

  A． 1 4 a + 1 4 b + 1 4 c	B． 1 2 a + 1 3 b + 1 4 c
  C． 1 3 a + 1 2 b + 1 4 c	D． 1 3 a + 1 4 b + 1 4 c
  組卷：216引用：8難度：0.8

  解析

• 4．若雙曲線

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  0

  ，

  b

  ＞

  0

  ）

  的焦點到漸近線的距離等于實軸長，則雙曲線的離心率為（　　）

  A． 2

  B． 3

  C． 5

  D．2
  組卷：134引用：9難度：0.9

  解析

• 5．（x+2y）（x-y）⁵的展開式中x²y⁴的系數為（　　）

  A．-15

  B．5

  C．-20

  D．25
  組卷：619引用：5難度：0.8

  解析

• 6．直線l的方向向量為

  m

  =

  （

  1

  ，

  0

  ，-

  1

  ）

  ，且l過點A（1，1，1），則點P（-1，2，1）到l的距離為（　　）

  A． 2

  B． 3

  C． 6

  D． 2 2
  組卷：784引用：6難度：0.7

  解析

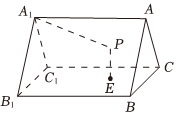• 7．如圖，直三棱柱ABC-A₁B₁C₁的所有棱長均相等，P是側面AA₁C₁C內一點，若點P到平面BB₁C₁C的距離

  |

  PE

  |

  =

  3

  2

  |

  P

  A

  1

  |

  ，則點P的軌跡是（　　）

  A．圓的一部分	B．橢圓的一部分
  C．雙曲線的一部分	D．拋物線的一部分
  組卷：51引用：2難度：0.5

  解析

四、解答題：本題共6小題，共70分．解答應寫出文字說明、證明過程或演算步驟．

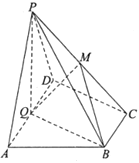• 21．如圖，在四棱錐P-ABCD中，底面ABCD為直角梯形，AD∥BC，∠ADC=90°，平面PAD⊥底面ABCD，Q為AD的中點，M是棱PC上的點，PA=PD=2，

  BC

  =

  1

  2

  AD

  =

  1

  ，

  CD

  =

  3

  ．
  （1）求證：平面MQB⊥平面PAD；
  （2）若

  PM

  =

  1

  3

  PC

  ，求異面直線AP與BM所成角的余弦值；
  （3）在線段PC上是否存在一點M，使二面角M-BQ-C大小為30°？若存在，請指出點M的位置，若不存在，請說明理由．
  組卷：141引用：1難度：0.5

  解析

• 22．已知橢圓C：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =1（a＞b＞0）的左、右頂點分別為A，B，O為坐標原點，直線l：x=1與C的兩個交點和O，B構成一個面積為

  6

  的菱形．
  （1）求C的方程．
  （2）圓E過O，B，交l于點M，N，直線AM，AN分別交C于另一點P，Q．
  ①求k_AP?k_AQ的值；
  ②證明：直線PQ過定點．
  組卷：307引用：4難度：0.6

  解析