當前位置：試卷中心 > 試卷詳情

2022-2023學年天津市崇化中學高二（上）期末數學試卷

發布：2024/12/15 2:0:1

1．直線l：
3
x-3y+1=0的傾斜角為（　　）
A．
π
3
B．
π
4
C．
π
6
D．
π
2
組卷：308引用：6難度：0.8
解析
2．已知等差數列{a_n}滿足a₃+a₆+a₈+a₁₁=12，則2a₉-a₁₁的值為（　　）
A．-3 B．3 C．-12 D．12
組卷：1026引用：6難度：0.7
解析
3．拋物線y=ax²的準線方程為y=1，則a的值為（　　）
A．
-
1
2
B．-2 C．
-
1
4
D．-4
組卷：296引用：4難度：0.7
解析
4．已知直線l的一個方向向量為
μ
=（-1，
3
），則直線l的斜率為（　　）
A．1 B．
3
C．
3
3
D．
-
3
組卷：353引用：5難度：0.7
解析
5．已知直線3x-6λy-5=0與直線2x-4y+3=0互相垂直，則實數λ=（　　）
A．4 B．
1
2
C．
-
1
4
D．
-
2
3
組卷：147引用：3難度：0.8
解析
6．已知雙曲線
C
：
x
2
a
2
-
y
2
b
2
=
1
（
a
＞
0
，
b
＞
0
）
的實軸長是虛軸長的3倍，則C的離心率為（　　）
A．
4
3
B．
10
3
C．
6
5
D．
2
3
3
組卷：300引用：3難度：0.7
解析
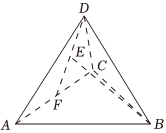7．在正四面體ABCD中，F是AC的中點，E是DF的中點，若
DA
=
a
，
DB
=
b
，
DC
=
c
，則
BE
=（　　）
A．
1
4
a
-
b
+
1
4
c
B．
1
2
a
-
b
+
1
2
c
C．
1
4
a
+
b
+
1
4
c
D．
1
2
a
-
b
+
c
組卷：821引用：7難度：0.7
解析

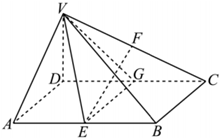22．如圖，已知四棱錐V-ABCD的底面是矩形，VD⊥平面ABCD，AB=2AD=2VD=2，E，F，G分別是棱AB，VC，CD的中點．
（1）求證：EF∥平面VAD；
（2）求平面AVE與平面VEG夾角的大小．
組卷：138引用：3難度：0.4
解析
23．橢圓
C
：
x
2
a
2
+
y
2
b
2
=
1
（a＞b＞0），直線y=k（x-1）經過橢圓C的一個焦點與其相交于點M，N，且點
A
（
1
，
3
2
）
在橢圓C上．
（I）求橢圓C的方程；
（II）若線段MN的垂直平分線與x軸相交于點P，問：在x軸上是否存在一個定點Q，使得
|
PQ
|
|
MN
|
為定值？若存在，求出點Q的坐標和
|
PQ
|
|
MN
|
的值；若不存在，說明理由．
組卷：175引用：8難度：0.3
解析