2022-2023學年黑龍江省大慶鐵人中學高二（下）期中數學試卷

一、單選題（每小題只有一個選項正確，共8小題，每小題5分，共40分。）

• 1．已知數列{a_n}為等差數列，且滿足a₁₀₀=2023，a₂₀₂₃=100，則a₂₁₂₃的值為（　　）

  A．2033

  B．2123

  C．123

  D．0
  組卷：110引用：3難度：0.7

  解析

• 2．設可導函數f（x）=lnx+x,則

  lim

  Δ

  x

  →

  0

  f

  （

  1

  +

  3

  Δ

  x

  ）

  -

  f

  （

  1

  ）

  Δ

  x

  =（　　）

  A．-2

  B．2

  C． 2 3

  D．6
  組卷：14引用：1難度：0.8

  解析

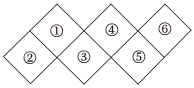• 3．用紅、黃、藍三種顏色給下圖著色，要求有公共邊的兩塊不著同色．在所有著色方案中，①③⑤著相同色的有（　　）

  A．96種

  B．24種

  C．48種

  D．12種
  組卷：173引用：6難度：0.7

  解析

• 4．對四組數據進行統計，獲得以下散點圖，關于其相關系數的比較，正確的是（　　）
  

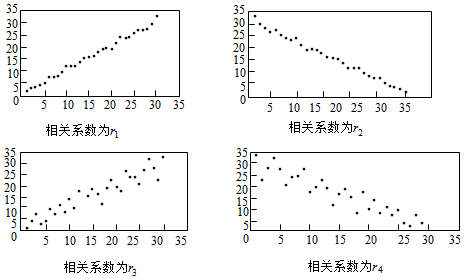
  A．r2＜r4＜0＜r3＜r1	B．r4＜r2＜0＜r1＜r3
  C．r4＜r2＜0＜r3＜r1	D．r2＜r4＜0＜r1＜r3
  組卷：1796引用：51難度：0.9

  解析

• 5．隨機變量X的概率分布規律為P（X=n）=

  a

  n

  （

  n

  +

  1

  ）

  （n=1，2，3，4），其中a是常數，則P（

  1

  2

  ＜X＜

  5

  2

  ）的值為（　　）

  A． 2 3

  B． 3 4

  C． 4 5

  D． 5 6
  組卷：1321引用：53難度：0.9

  解析

• 6．若

  A

  2

  2

  n

  =

  A

  2

  3

  A

  2

  n

  ，

  C

  x

  9

  =

  C

  2

  x

  9

  ，則x+n=（　　）

  A．5

  B．3

  C．6

  D．2或5
  組卷：54引用：1難度：0.8

  解析

• 7．用1、2、3、4、5組成沒有重復數字的五位數

  abcde

  ，（

  abcde

  代表萬位，千位，百位，十位，個位依次為a,b,c,d,e）其中滿足a＞b＞c＜d＜e的五位數有n個．則在1+（1+x）¹+（1+x）²+（1+x）³+?+（1+x）ⁿ的展開式中，x²的系數是（　　）

  A．56

  B．35

  C．20

  D．84
  組卷：41引用：3難度：0.7

  解析

四、解答題（本題共6小題，共70分，解答應寫出必要的文字說明、證明過程及演算步驟）

• 21．某技術部門對工程師進行達標等級考核，需要進行兩輪測試，每輪測試的成績在90分及以上的定為該輪測試通過，只有通過第一輪測試的人員才能進行第二輪測試，兩輪測試的過程相互獨立，并規定：
  ①兩輪測試均通過的定為一級工程師；
  ②僅通過第一輪測試，而第二輪測試沒通過的定為二級工程師；
  ③第一輪測試沒通過的不予定級．
  現有某公司的甲、乙、丙三位工程師參加等級考核，已知他們通過第一輪測試的概率分別為

  1

  3

  ，

  2

  3

  ，

  2

  3

  ，通過第二輪測試的概率均為

  1

  2

  ．
  （1）求經過本次考核，甲，乙，丙三位工程師中恰有兩位被定為一級工程師的概率；
  （2）公司為鼓勵工程師參加等級考核設制兩套獎勵方案：
  方案一：獎勵定為一級工程師2000元，獎勵定為二級工程師1500元，未定級給予鼓勵獎500元；
  方案二：獲得一級或二級工程師均獎勵2000元，未獲得任何等級的不予獎勵．
  采用哪套方案，公司的獎勵支出會更少？
  組卷：23引用：2難度：0.5

  解析

• 22．已知函數f（x）=ae^2x+（a-2）e^x-x.
  （1）當a=2時，求f（x）在x=0處的切線方程；
  （2）若f（x）有兩個零點，求a的取值范圍；
  （3）求證：

  e

  2

  x

  -

  x

  ＞

  e

  6

  （

  x

  3

  +

  3

  x

  +

  2

  ）

  ．
  組卷：242引用：4難度：0.3

  解析