2023-2024學年陜西省西安市鐵一中學高二（上）期中數學試卷

一、單項選擇題．本題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求．

• 1．已知

  sinα

  =

  1

  3

  ，

  α

  ∈

  （

  π

  2

  ，

  π

  ）

  ，則tanα的值為（　　）

  A． - 2 4

  B． 2 4

  C． - 2 2

  D． 2 2
  組卷：1282引用：8難度：0.8

  解析

• 2．已知a＞0，b＞0且2ab=a+2b,則a+8b的最小值為（　　）

  A． 4 2

  B．10

  C．9

  D． 27 2
  組卷：97引用：2難度：0.7

  解析

• 3．函數f（x）=sinx?ln|x|的部分圖象大致為（　　）

  A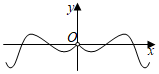．	B．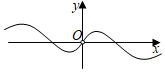
  C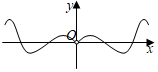．	D．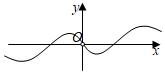
  組卷：354引用：11難度：0.9

  解析

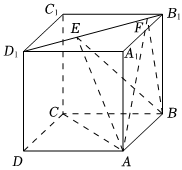• 4．如圖，正方體ABCD-A₁B₁C₁D₁的棱長為1，線段B₁D₁上有兩個動點E，F，且EF=

  2

  2

  ，則下列結論中錯誤的是（　　）

  A．AC⊥BE

  B．EF∥平面ABCD

  C．直線AB與平面BEF所成的角為定值

  D．異面直線AE，BF所成的角為定值
  組卷：403引用：8難度：0.7

  解析

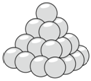• 5．宋代制酒業很發達，為了存儲方便，酒缸是要一層一層堆起來的，形成堆垛，用簡便的方法算出堆垛中酒缸的總數，古代稱之為堆垛術．有這么一道關于“堆垛”求和的問題：將半徑相等的圓球堆成一個三角垛，底層是每邊為n個圓球的三角形，向上逐層每邊減少一個圓球，頂層為一個圓球，記自上而下第n層的圓球總數為a_n，容易發現：a₁=1，a₂=3，a₃=6，則a₁₀-a₅=（　　）

  A．45

  B．40

  C．35

  D．30
  組卷：61引用：4難度：0.7

  解析

• 6．已知焦點為F₁，F₂的雙曲線C的離心率為

  5

  ，點P為C上一點，且滿足2|PF₁|=3|PF₂|，若△PF₁F₂的面積為

  2

  5

  ，則雙曲線C的實軸長為（　　）

  A．2

  B． 2

  C． 2 2

  D． 2 2
  組卷：326引用：4難度：0.5

  解析

• 7．已知△ABC的三個頂點都在拋物線x²=6y上，且F為拋物線的焦點，若

  AF

  =

  1

  3

  （

  AB

  +

  AC

  ）

  ，則

  |

  AF

  |

  +

  |

  BF

  |

  +

  |

  CF

  |

  =（　　）

  A．12

  B．10

  C．9

  D．6
  組卷：77引用：2難度：0.6

  解析

四、解答題：本題共6小題，共70分．解答應寫出文字說明、證明過程或演算步驟．

• 21．已知數列{a_n}滿足a₁=2，

  a

  n

  +

  1

  =

  2

  -

  1

  a

  n

  （

  n

  ∈

  N

  *

  ）

  ．
  （1）設

  b

  n

  =

  1

  a

  n

  -

  1

  ，求證：數列{b_n}為等差數列，并求數列{a_n}的通項公式；
  （2）設

  c

  n

  =

  2

  a

  n

  n

  +

  1

  ，數列{c_nc_n+2}的前n項和為T_n，是否存在正整數m,使得

  T

  n

  ＜

  1

  c

  m

  c

  m

  +

  1

  對任意的n∈N^*都成立？若存在，求出m的最小值；若不存在，試說明理由．
  組卷：205引用：5難度：0.4

  解析

• 22．已知橢圓C：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =1（a＞b＞0）的長軸長為8，以橢圓的左焦點為圓心，短半軸長為半徑的圓與直線h：y=

  2

  2

  （x-4）直線相切．
  （1）求橢圓的方程C；
  （2）已知直線l：x=8，過右焦點F的直線（不與軸重合）與橢圓C交于A，B兩點，過點A作AD⊥l,垂足為D．
  ①求證：直線BD過定點E，并求出定點E的坐標；
  ②點O為坐標原點，求△OBD面積的最大值．
  組卷：145引用：4難度：0.6

  解析