2022-2023學(xué)年福建省泉州一中七年級(jí)（下）期中數(shù)學(xué)試卷

一、選擇題（共40分）

• 1．下列方程中，是二元一次方程的是（　　）

  A．2x+3y=5	B．xy=1
  C． 2 （ m - 5 ） = 1 4 m - 2	D． 1 - 2 3 m = n
  組卷：804引用：9難度：0.7

  解析

• 2．已知m=2是方程2m-3a=1的解，則a的值是（　　）

  A．1

  B． 7 2

  C． - 5 3

  D． - 5 2
  組卷：115引用：4難度：0.8

  解析

• 3．在數(shù)軸上表示不等式-1＜x≤2，正確的是（　　）

  A．

  B．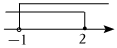

  C．

  D．
  組卷：42引用：3難度：0.8

  解析

• 4．下列方程的變形中，正確的是（　　）

  A．方程3m=2m-1，移項(xiàng)得3m+2m=1

  B．方程3=2-5（x-1），去括號(hào)得3=2-5x-1

  C．方程 x - 1 2 - x 5 = 1 ，可化為5（x-1）-2x=10

  D．方程 x - 1 0 . 2 - x + 1 0 . 5 = 1 ，可化為 x - 1 2 - x + 1 5 = 10
  組卷：1647引用：9難度：0.8

  解析

• 5．下列判斷不正確的是（　　）

  A．若a＞b,則a+2＞b+2	B．若a＞b,則-2a＜-2b
  C．若2a＞2b,則a＞b	D．若a＞b,則ac2＞bc2
  組卷：1371引用：8難度：0.8

  解析

• 6．在解二元一次方程組

  6 x + my = 3 ①

  2 x - ny = - 6 ②

  時(shí)，若①-②可直接消去未知數(shù)y,則m和n滿足下列條件是（　　）

  A．m=n

  B．mn=1

  C．m+n=0

  D．m+n=1
  組卷：1309引用：13難度：0.6

  解析

• 7．程大位是我國明朝商人，珠算發(fā)明家．他60歲時(shí)完成的《直指算法統(tǒng)宗》是東方古代數(shù)學(xué)名著，詳述了傳統(tǒng)的珠算規(guī)則，確立了算盤用法．書中有如下問題：一百饅頭一百僧，大僧三個(gè)更無爭，小僧三人分一個(gè)，大小和尚得幾丁．意思是：有100個(gè)和尚分100個(gè)饅頭，如果大和尚1人分3個(gè)，小和尚3人分1個(gè)，正好分完，大、小和尚各有多少人？若設(shè)大和尚有x人，則列出的方程正確的是（　　）

  A． 3 x + x 3 = 100	B． x 3 + 3 （ 100 - x ） = 100
  C． 3 x + 100 - x 3 = 100	D． x 3 + 100 - 3 x = 100
  組卷：1126引用：11難度：0.7

  解析

• 8．已知關(guān)于x的一元一次方程

  x

  2023

  +

  5

  =

  2023

  x

  +

  m

  的解為x=2018，那么關(guān)于x的一元一次方程

  x

  -

  5

  2023

  -

  5

  =

  2023

  （

  x

  -

  5

  ）

  -

  m

  的解為x=（　　）

  A．2013

  B．-2013

  C．2023

  D．-2023
  組卷：331引用：2難度：0.7

  解析

三、解答題（共86分）

• 24．用如圖1所示的A，B兩種紙板作側(cè)面或底面制作如圖2所示的甲、乙兩種長方體形狀的無蓋紙盒．
  
  （1）現(xiàn)有A紙板70張，B型紙板160張，要求恰好用完所有紙板，問可制作甲、乙兩種無蓋紙盒各多少個(gè)？
  （2）若現(xiàn)倉庫A型紙板較為充足，B型紙板只有30張，根據(jù)現(xiàn)有的紙板最多可以制作多少個(gè)如圖2所示的無蓋紙盒（甲、乙兩種都有，要求B型紙板用完）；
  （3）經(jīng)測(cè)量發(fā)現(xiàn)B型紙板的長是寬的2倍（即b=2a），若倉庫有6個(gè)丙型的無蓋大紙盒（長寬高分別為2a,a,2a），現(xiàn)將6個(gè)丙型無蓋大紙盒經(jīng)過拆剪制作成甲、乙兩種型號(hào)的紙盒，可以各做多少個(gè)（假設(shè)沒有邊角消耗，沒有余料）？
  組卷：410引用：3難度：0.5

  解析

• 25．一個(gè)四位數(shù)，記千位數(shù)字與個(gè)位數(shù)字之和為x,十位數(shù)字與百位數(shù)字之和為y,如果x=y,那么稱這個(gè)四位數(shù)為“一峰數(shù)”．
  （1）最大的“一峰數(shù)”為

  ，最小的“一峰數(shù)”為

  ；
  （2）對(duì)x,y定義新的運(yùn)算F，規(guī)定：

  F

  （

  x

  ,

  y

  ）

  =

  x - y （ x ≥ y ）

  y - x （ x ＜ y ）

  時(shí)，若正數(shù)x滿足不等式組

  F （ x , 4 ） ＞ 1

  F （ - 4 ， x ） ≤ 6

  ，則這樣的“一峰數(shù)”有哪幾個(gè)，并請(qǐng)求出來；
  （3）一個(gè)“一峰數(shù)”M，它的百位數(shù)字是千位數(shù)字a的3倍，個(gè)位數(shù)字與十位數(shù)字之和為10，且個(gè)位數(shù)字b能使得不等式組

  3 x - 4 4 - 1 ≤ x - 2 2

  8 x - 1 ＞ b

  恰有3個(gè)整數(shù)解，求出所有滿足條件的“一峰數(shù)”M的值．
  組卷：706引用：4難度：0.5

  解析