2022-2023學年廣東省汕頭市高三（上）質檢數學試卷（12月份）

一、單項選擇題：本題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的．

• 1．已知集合A={x|x≥0}，集合B={x|x＞1}，則以下命題正確的是（　　）

  A．?x∈A，x?B

  B．?x∈B，x?A

  C．?x∈A，x∈B

  D．?x∈B，x∈A
  組卷：143引用：5難度：0.9

  解析

• 2．已知復數z滿足（1+2i）z=2+i,則|z|=（　　）

  A． 5 5

  B．1

  C． 5

  D．5
  組卷：49引用：3難度：0.9

  解析

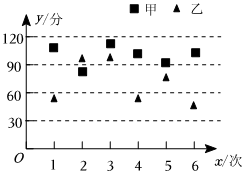• 3．已知甲、乙兩名同學在高三的6次數學測試的成績統計如圖（圖標中心點所對縱坐標代表該次數學測試成績），則下列說法不正確的是（　　）

  A．甲成績的極差小于乙成績的極差

  B．甲成績的第25百分位數大于乙成績的第75百分位數

  C．甲成績的平均數大于乙成績的平均數

  D．甲成績的方差小于乙成績的方差
  組卷：113引用：5難度：0.8

  解析

• 4．已知等差數列{a_n}且3（a₃+a₅）+2（a₇+a₁₀+a₁₃）=48，則數列{a_n}的前13項之和為（　　）

  A．24

  B．39

  C．104

  D．52
  組卷：41引用：3難度：0.7

  解析

• 5．已知某運動員每次射擊擊中目標的概率是p,假設每次射擊擊中目標與否互不影響，設ξ為該運動員n次射擊練習中擊中目標的次數，且E（ξ）=8，D（ξ）=1.6，則p值為（　　）

  A．0.6

  B．0.8

  C．0.9

  D．0.92
  組卷：63引用：3難度：0.8

  解析

• 6．如圖1，在高為h的直三棱柱容器ABC-A₁B₁C₁中，AB=AC=2，AB⊥AC．現往該容器內灌進一些水，水深為2，然后固定容器底面的一邊AB于地面上，再將容器傾斜，當傾斜到某一位置時，水面恰好為A₁B₁C（如圖2），則容器的高h為（　　）

  A．3

  B．4

  C． 4 2

  D．6
  組卷：644引用：14難度：0.8

  解析

• 7．（x+3y）（x-2y）⁶的展開式中x⁵y²的系數為（　　）

  A．60

  B．24

  C．-12

  D．-48
  組卷：771引用：6難度：0.8

  解析

四、解答題：本題共6小題，共70分．解答應寫出文字說明、證明過程或演算步驟．

• 21．已知函數

  f

  （

  x

  ）

  =

  lnx

  -

  1

  2

  a

  x

  2

  +

  （

  a

  -

  1

  ）

  x

  ，a∈R．
  （1）討論f（x）的單調性；
  （2）曲線y=f（x）上是否存在不同兩點A（x₁，y₁）、B（x₂，y₂），使得直線AB與曲線y=f（x）在點

  （

  x

  1

  +

  x

  2

  2

  ，

  f

  （

  x

  1

  +

  x

  2

  2

  ）

  ）

  處的切線平行？若存在，求出A、B坐標，若不存在，請說明理由．
  組卷：6引用：2難度：0.5

  解析

• 22．已知橢圓

  C

  1

  ：

  x

  2

  4

  +

  y

  2

  =

  1

  的左、右頂點分別為A₁、A₂，上、下頂點分別為B₁、B₂，記四邊形A₁B₁A₂B₂的內切圓為C₂，過橢圓C₁上一點T引圓C₂的兩條切線（切線斜率存在且不為0），分別交橢圓C₁于點P、Q．
  （1）試探究直線TP與TQ斜率之積是否為定值，并說明理由；
  （2）記點O為坐標原點，求證：P、O、Q三點共線．
  組卷：64引用：3難度：0.3

  解析