2023-2024學年廣東省廣州市奧林匹克中學高二（上）期中數學試卷

一、單選題。（本大題8個小題，每小題5分，共40分。在每小題給出的四個選項中，只有一項是符合題目要求的）

• 1．已知圓

  C

  1

  ：

  （

  x

  -

  1

  ）

  2

  +

  （

  y

  +

  1

  ）

  2

  =

  2

  ，圓

  C

  2

  ：

  （

  x

  +

  2

  ）

  2

  +

  （

  y

  -

  3

  ）

  2

  =

  9

  ，則這兩圓的位置關系是（　　）

  A．外離

  B．外切

  C．相交

  D．內含
  組卷：32引用：1難度：0.7

  解析

• 2．已知向量

  a

  =

  （

  λ

  +

  1

  ，

  0

  ，

  2

  ）

  ，

  b

  =

  （

  3

  λ

  ，

  2

  μ

  -

  1

  ，

  1

  ）

  ，若

  a

  ∥

  b

  ，則λ+μ=（　　）

  A． - 7 10

  B． 7 10

  C．-7

  D．7
  組卷：60引用：1難度：0.7

  解析

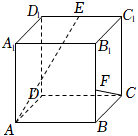• 3．正方體ABCD-A₁B₁C₁D₁中，E，F分別為D₁C₁，BB₁的中點，則異面直線AE與FC所成角的余弦值為（　　）

  A． 5 15

  B． 4 5 15

  C． - 2 5 15

  D． 2 5 15
  組卷：324引用：7難度：0.6

  解析

• 4．若直線（a+2）x+（1-a）y-3=0與直線（a-1）x+（2a+3）y+2=0互相垂直．則a的值為（　　）

  A．1

  B．-1

  C．±1

  D．- 3 2
  組卷：335引用：17難度：0.9

  解析

• 5．在棱長為1的正四面體ABCD中，E，F分別是BC，AD中點，則

  AE

  ?

  CF

  =（　　）

  A．0

  B． 1 2

  C． - 3 4

  D． - 1 2
  組卷：156引用：14難度：0.7

  解析

• 6．已知點A（-1，0），B（2，3），點P是直線y=x-1上的動點，則|PA|+|PB|的最小值是（　　）

  A． 3 2

  B． 2 + 10

  C．5

  D． 26
  組卷：80引用：1難度：0.8

  解析

• 7．若函數y=-

  4

  -

  （

  x

  -

  1

  ）

  2

  的圖象與直線x-2y+m=0有公共點，則實數m的取值范圍為（　　）

  A．[-2 5 -1，-2 5 +1]	B．[-2 5 -1，1]
  C．[-2 5 +1，-1]	D．[-3，1]
  組卷：1184引用：18難度：0.8

  解析

四、解答題。（第17題10分，18-22題每題12分，共70分）

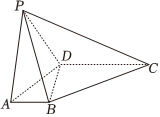• 21．在四棱錐P-ABCD中，平面ABCD⊥平面PCD，底面ABCD為直角梯形，AB∥CD，AD⊥DC，且AB=1，AD=DC=DP=2，?∠PDC=120°．
  （1）求證：AD⊥平面PCD；
  （2）線段BC上是否存在點F，使得平面PDF⊥平面PAC？如果存在，求

  BF

  BC

  的值；如果不存在，說明理由．
  組卷：142引用：1難度：0.4

  解析

• 22．已知圓M：x²+（y-4）²=4，點P是直線l：x-2y=0上的一動點，過點P作圓M的切線PA、PB，切點為A、B．
  （Ⅰ）當切線PA的長度為2

  3

  時，求點P的坐標；
  （Ⅱ）若△PAM的外接圓為圓N，試問：當P運動時，圓N是否過定點？若存在，求出所有的定點的坐標；若不存在，說明理由；
  （Ⅲ）求線段AB長度的最小值．
  組卷：987引用：27難度：0.3

  解析