2022-2023學年江蘇省無錫市濱湖區金橋雙語實驗學校八年級（上）期中數學試卷

一．選擇題（共10小題）

• 1．2022年冬奧會將在北京舉行，中國將是第一個實現奧運“全滿貫”（先后舉辦奧運會、殘奧會、青奧會、冬奧會、冬殘奧會）的國家．以下會徽是軸對稱圖形的是（　　）

  A．

  B．

  C．

  D．
  組卷：310引用：15難度：0.9

  解析

• 2．下列計算正確的是（　　）

  A． 4 =±2

  B． （ - 3 ） 2 =-3

  C． 3 9 = 3

  D． 3 0 . 064 =0.4
  組卷：263引用：4難度：0.8

  解析

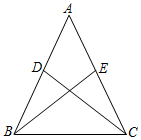• 3．如圖，在△ABC中，AB=AC，D、E兩點分別在邊AB、AC上．添加一個條件，仍不能判定△ABE≌△ACD，則這個條件是（　　）

  A．AE=AD

  B．∠ABE=∠ACD

  C．BE=CD

  D．BD=CE
  組卷：62引用：2難度：0.7

  解析

• 4．下列命題中正確的是（　　）

  A．數軸上的點與實數一一對應

  B．無理數是帶根號的數

  C．無限小數都是無理數

  D．零是最小的實數
  組卷：234引用：4難度：0.7

  解析

• 5．小明同學在學習了全等三角形的相關知識后發現，只用兩把完全相同的長方形直尺就可以作出一個角的平分線．如圖，一把直尺壓住射線OB，另一把直尺壓住射線OA并且與第一把直尺交于點P，小明說：“射線OP就是∠BOA的平分線．”他這樣做的依據是（　　）

  A．角平分線上的點到這個角兩邊的距離相等

  B．角的內部到角的兩邊的距離相等的點在角的平分線上

  C．三角形三條角平分線的交點到三條邊的距離相等

  D．以上均不正確
  組卷：579引用：19難度：0.5

  解析

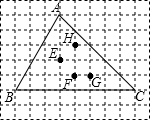• 6．在正方形網格中，△ABC的位置如圖所示，且頂點在格點上，在△ABC內部有E、F、G、H四個格點，到△ABC三個頂點距離相等的點是（　　）

  A．點E

  B．點F

  C．點G

  D．點H
  組卷：2088引用：22難度：0.8

  解析

• 7．如圖，已知△ABC中，∠ABC=90°，AB=BC，三角形的頂點在相互平行的三條直線l₁，l₂，l₃上，且l₁，l₂之間的距離為1，l₂，l₃之間的距離為2，則AC²=（　　）

  A．13

  B．20

  C．26

  D．25
  組卷：550引用：10難度：0.7

  解析

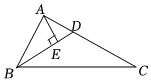• 8．如圖，在△ABC中，BD為∠ABC的平分線，AE⊥BD，垂足為E，且AB=5，AE=3，BC=11，則∠BAE與∠C的關系為（　　）

  A．∠BAE=3∠C	B．∠BAE+2∠C=90°
  C．∠BAE=2∠C	D． 1 2 ∠BAE+∠C=90°
  組卷：693引用：3難度：0.9

  解析

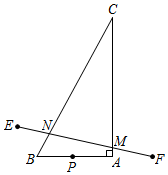• 9．如圖，Rt△ABC中，∠A=90°，∠C=30°，AB=1，AC=

  3

  ，動點P在邊AB上（不與A、B重合），點P關于BC，AC的對稱點分別為點E，F，連接EF，交AC，BC分別為點M，N．
  甲：我發現線段EF的最大值為2，最小值為

  3

  ；
  乙：我連接PM，PN，發現△PMN一定為鈍角三角形．
  則下列判斷正確的是（　　）

  A．甲對乙對

  B．甲對乙錯

  C．甲錯乙對

  D．甲錯乙錯
  組卷：365引用：4難度：0.6

  解析

三．解答題

• 26．若△ABC和△ADE均為等腰三角形，且AB=AC=AD=AE，當∠ABC和∠ADE互余時，稱△ABC與△ADE互為“底余等腰三角形”，△ABC的邊BC上的高AH叫做△ADE的“余高”．
  （1）如圖1，△ABC與△ADE互為“底余等腰三角形”．
  ①若連接BD，CE，判斷△ABD與△ACE是否互為“底余等腰三角形”：

  （填“是”或“否”）；
  ②當∠BAC=90°時，若△ADE的“余高”AH=

  5

  ，則DE=

  ；
  ③當0°＜∠BAC＜180°時，判斷DE與AH之間的數量關系，并證明；
  （2）如圖2，在四邊形ABCD中，∠ABC=60°，DA⊥BA，DC⊥BC，且DA=DC．
  ①畫出△OAB與△OCD，使它們互為“底余等腰三角形”；
  ②若△OCD的“余高”長為a,則點A到BC的距離為

  （用含a的式子表示）．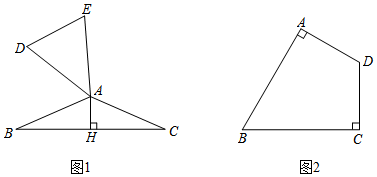
  
  組卷：651引用：5難度：0.3

  解析

• 27．小明在一次數學興趣小組活動中，對一個數學問題做如下探究：
  【問題背景】
  如圖①，在四邊形ADBC中，∠ACB=∠ADB=90°，AD=BD，探究線段AC、BC、CD之間的數量關系．小明同學探究此問題的思路是：將△BCD繞點D逆時針旋轉90°到△AED處，點B、C分別落在點A、E處（如圖②），易證點C、A、E在同一條直線上，并且△CDE是等腰直角三角形，所以CE=CD，從而得出結論：AC+BC=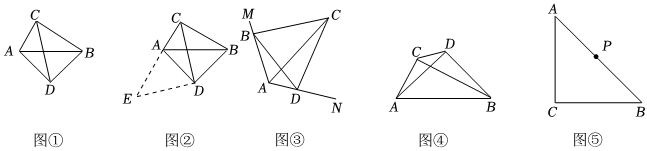

  2

  CD．
  
  【簡單應用】
  （1）在圖①中，若AB=5，BC=4，則CD²=

  ．
  （2）如圖③，在四邊形ABCD中，∠BAD=120°，點B和點D分別在邊AM和AN上移動，且滿足∠BCD與∠BAD互補，CB=CD，AC=6，則以下結論：
  ①AB+AD的值不變；
  ②∠BAC=∠DAC恒成立；
  ③BD的長不變；
  ④四邊形ABCD的面積不變，其中正確的序號有

  ．
  【拓展延伸】
  （3）如圖④，∠ACB=∠ADB=90°，AD=BD，若AC=a,BC=b（a＜b），求CD²的長．（用含a、b的代數式表示）．
  （4）如圖⑤，∠ACB=90°，AC=BC=13，點P為AB的中點，若點E滿足AE=10，CE=CA，點Q為AE的中點，則PQ²=

  ．
  組卷：431引用：1難度：0.3

  解析