2021-2022學年云南省昆明一中高一(下)期中數學試卷
發布:2024/4/20 14:35:0
一、單項選擇題。本題共8小題,每小題5分,共40分.在每小題給出的四個選項中,只有一項是符合題目要求的。
-
1.已知z=2+i,其中i為虛數單位,則在復平面內z的共軛復數對應的點位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限 組卷:45引用:4難度:0.8 -
2.若cos(
-α)=π4,則sin2α=( )35A. 725B. 15C.- 15D.- 725組卷:12476引用:109難度:0.7 -
3.已知向量
,a滿足|b|=|a|=|b|=2,則|2a+b+a|=( )bA.2 7B.2 C.2 3D.2 5組卷:834引用:2難度:0.7 -
4.如圖,在梯形ABCD中,CD∥AB,AB=2CD,P是BC中點,則
=( )AP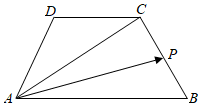
A. 12AD+13DCB. 12AD+DCC. 32DC+12ADD. 12AD+32DC組卷:192引用:2難度:0.7 -
5.在邊長為3的等邊△ABC中,點M滿足
=BM,則2MA=( )CM?CAA. 32B. 23C.6 D. 152組卷:216引用:5難度:0.9 -
6.已知O是△ABC內一點,滿足
,則S△ABC:S△OBC=( )AO=23(AB+12BC)A.3:1 B.1:3 C.2:1 D.1:2 組卷:1006引用:5難度:0.8 -
7.已知
,且|a|=1,|b|=2,則向量a⊥(a+b)在a方向上的投影向量為( )bA. -22bB. 22bC. 12bD. -12b組卷:84引用:1難度:0.6
四、解答題。(本大題共6個小題,共70分,其中17題10分,其余每題12分)各題解答必須答在答題卷上相應題目指定的方框內(必須寫出必要的文字說明、演算步驟或推理過程).
-
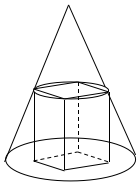 21.如圖所示是在圓錐內部挖去一正四棱柱所形成的幾何體,該正四棱柱上底面的四頂點在圓錐側面上,下底面落在圓錐底面內,已知圓錐側面積為15π,底面半徑為r=3.
21.如圖所示是在圓錐內部挖去一正四棱柱所形成的幾何體,該正四棱柱上底面的四頂點在圓錐側面上,下底面落在圓錐底面內,已知圓錐側面積為15π,底面半徑為r=3.
(Ⅰ)若正四棱柱的底面邊長為a=,求該幾何體的體積;2
(Ⅱ)求該幾何體內正四棱柱側面積的最大值.組卷:295引用:6難度:0.6 -
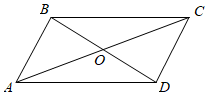 22.如圖,在平行四邊形ABCD中,BD,AC相交于點O,設向量=AB,a=AD.b
22.如圖,在平行四邊形ABCD中,BD,AC相交于點O,設向量=AB,a=AD.b
(1)若AB=1,AD=2,∠BAD=60°,證明:;AB⊥BD
(2)若點P是平行四邊形ABCD所在平面內一點,且滿足5,求△ACP與△ACD的面積的比;AP=AC+3AD
(3)若AB=AD=2,∠BAD=60°,點E,F分別在邊AD,CD上,,AE=λAD,且CF=μCD,求λ+μ的值.BE?BF=1,DE?DF=-23組卷:414引用:2難度:0.1


