2022-2023學年北京十九中高一（下）期中數學試卷

一、選擇題（本大題共10道小題，每小題6分，共60分．在每小題給出的四個選項中，只有一項是符合題目要求的，請把正確答案填涂在答題紙相應位置上．）

• 1．已知

  a

  =（-3，3），

  b

  =（6，x），若

  a

  與

  b

  共線，則x等于（　　）

  A．6

  B．-6

  C．3

  D．-3
  組卷：150引用：3難度：0.5

  解析

• 2．已知α∈（0，π），且cosα=-

  3

  5

  ，則tanα等于（　　）

  A． - 4 3

  B． - 3 4

  C． 3 4

  D． 4 3
  組卷：789引用：16難度：0.9

  解析

• 3．已知函數f（x）=cos（2x+φ），則“

  φ

  =

  π

  2

  ”是“f（x）是奇函數”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充要條件	D．既不充分也不必要條件
  組卷：65引用：4難度：0.7

  解析

• 4．為得到函數

  y

  =

  sin

  （

  2

  x

  +

  π

  4

  ）

  的圖象，只需將函數y=sinx的圖象（　　）
  ①向左平移

  π

  4

  個單位長度，再將每個點的橫坐標縮短為原來的

  1

  2

  ；
  ②向右平移

  π

  8

  個單位長度，再將每個點的橫坐標縮短為原來的

  1

  2

  ；
  ③每個點的橫坐標縮短為原來的

  1

  2

  ，再向右平移

  π

  8

  個單位長度；
  ④每個點的橫坐標縮短為原來的

  1

  2

  ，再向左平移

  π

  8

  個單位長度．

  A．①④

  B．①③

  C．②④

  D．②③
  組卷：236引用：3難度：0.7

  解析

• 5．我國著名數學家華羅庚先生曾說：數缺形時少直觀，形缺數時難入微，數形結合百般好，隔裂分家萬事休，在數學的學習和研究中，函數的解析式常用來琢磨函數圖象的特征．函數

  f

  （

  x

  ）

  =

  ln

  |

  x

  |

  ?

  cosx

  x

  +

  sinx

  在[-π，0）∪（0，π]的圖象大致為（　　）

  A．	B．
  C．	D．
  組卷：184引用：3難度：0.8

  解析

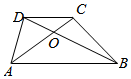• 6．如圖，梯形ABCD中，AB∥CD，且AB=2CD，對角線AC、DB相交于點O．若

  AD

  =

  a

  ，

  AB

  =

  b

  ，

  OC

  =（　　）

  A． a 3 - b 6

  B． a 3 + b 6

  C． 2 a 3 + b 3

  D． 2 a 3 - b 3
  組卷：485引用：7難度：0.7

  解析

三．解答題（本大題共4道小題，共54分．請把解題過程寫在答題紙相應位置上．）

• 19．已知函數

  f

  （

  x

  ）

  =

  sin

  （

  2

  x

  +

  π

  6

  ）

  ．
  （Ⅰ）請用“五點法”畫出函數f（x）在一個周期上的圖象；
  （Ⅱ）求f（x）在區間

  [

  π

  12

  ，

  π

  2

  ]

  上的最大值和最小值；
  （Ⅲ）寫出f（x）的單調遞增區間．
  
  組卷：485引用：4難度：0.7

  解析

• 20．若函數f（x）滿足f（x）=f（x+

  3

  π

  2

  ）且f（

  π

  4

  +x）=f（

  π

  4

  -x）（x∈R），則稱函數f（x）為“M函數”．
  （1）試判斷f（x）=sin

  4

  3

  x是否為“M函數”，并說明理由；
  （2）函數f（x）為“M函數”，且當x∈[

  π

  4

  ，π]時，f（x）=sinx,求y=f（x）的解析式，并寫出在[0，

  3

  π

  2

  ]上的單調遞增區間；
  （3）在（2）的條件下，當x∈[

  -

  π

  2

  ，

  3

  kπ

  2

  +π]（k∈N）時，關于x的方程f（x）=a（a為常數）有解，記該方程所有解的和為S（k），求S（3）．
  組卷：249引用：6難度：0.6

  解析