2022-2023學年江蘇省無錫市惠山區陽山中學九年級（上）期中數學試卷
發布：2024/10/22 9:0:2
一、選擇題（本大題共10小題，每小題3分，共30分．在每小題所給出的四個選項中，只有一項是正確的，請用2B鉛筆把答題卡上相應的選項標號涂黑）
-
1．已知點P是線段AB的黃金分割點（AP＞PB），若AB=10，則AP的長約為（ ）
組卷：633引用：5難度：0.8 -
2．已知⊙O的半徑為4，OA=5，則點A在（ ）
組卷：463引用：9難度：0.8 -
3．若a是從“-1、0、1、2”這四個數中任取的一個數，則關于x的方程（a-1）x2+x-3=0為一元二次方程的a的值有（ ）個
組卷：21引用：2難度：0.5 -
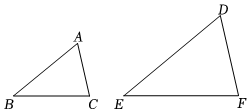4．如圖，△ABC和△DEF中，∠A=∠D，則添加下列條件后無法判定△ABC∽△DEF的是（ ）組卷：469引用：5難度：0.7 -
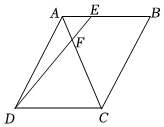5．如圖，在?ABCD中，E是AB上一點，且BE=2AE，連接DE交AC于點F，已知S△AFE=1，則S△ADC的值是（ ）組卷：645引用：3難度：0.5 -
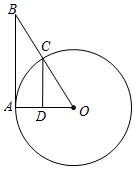6．如圖，已知⊙O的半徑為1，AB與⊙O相切于點A，OB與⊙O交于點C，CD⊥OA，垂足為D，則cos∠AOB的值等于（ ）組卷：239引用：2難度：0.7 -
7．在圓內接四邊形ABCD中，∠A、∠B、∠C的度數之比為2：4：7，則∠B的度數為（ ）
組卷：427引用：3難度：0.7 -
8．定義一種新運算：a⊕b=2a+b,a※b=a2b,則方程（x+1）※2=（3⊕x）-2的解是（ ）
組卷：860引用：4難度：0.7 -
9．平面直角坐標系內，已知點A（1，0），B（5，0），C（0，t）．當t＞0時，若∠ACB最大，則t的值為（ ）組卷：1595引用：3難度：0.5
三、解答題（本大題共10小題，共96分.請在答題卡指定區域內作答，解答時應寫出文字說明、證明過程或演算步驟）
-
27．如圖，在△ABC中，∠BCA=90°，BC=8，AC=6，點D是AB邊上的中點，點E是BC邊上的一個動點，連接DE，將△BDE沿DE翻折得到△FDE．
（1）如圖①，線段DF與線段BC相交于點G，當BE=2時，則=；GEGD
（2）如圖②，當點E與點C重合時，線段EF與線段AB相交于點P，求DP的長；
（3）如圖③，連接CD，線段EF與線段CD相交于點M，當△DFM為直角三角形時，求BE的長．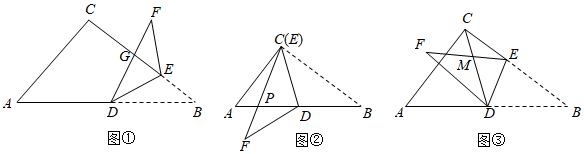
組卷：1109引用：8難度：0.2 -
28．蘇科版教材八年級下冊第94頁第19題，小明在學過圓之后，對該題進行重新探究，請你和他一起完成問題探究．
【問題提出】如圖1，點E，F分別在方形ABCD中的邊AD、AB上，且BE=CF，連接BE、CF交于點M，求證：BE⊥CF．請你先幫小明加以證明．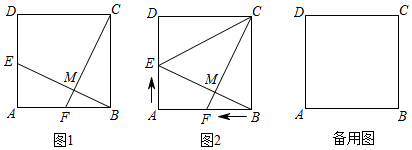
【問題探究】小明把原問題轉化為動點問題，如圖1，在邊長為6cm的正方形ABCD中，點E從點A出發，沿邊AD向點D運動，同時，點F從點B出發，沿邊BA向點A運動，它們的運動速度都是2cm/s,當點E運動到點D時，兩點同時停止運動，連接CF、BE交于點M，設點E，F運動時間為t秒．
（1）如圖1，在點E、F的運動過程中，點M也隨之運動，請直接寫出點M的運動路徑長 cm.
（2）如圖2，連接CE，在點E、F的運動過程中．
①試說明點D在△CME的外接圓⊙O上；
②若①中的⊙O與正方形的各邊共有6個交點，請直接寫出t的取值范圍．組卷：383引用：3難度：0.2