2022年天津市部分區高考數學質檢試卷（一）

一、選擇題：在每小題給出的四個選項中，只有一項是符合題目要求的．

• 1．已知集合A={-1，0，1}，B={x|x（x-2）≤0}，那么A∩B=（　　）

  A．{-1}

  B．{0，1}

  C．{0，1，2}

  D．{x|0≤x≤1}
  組卷：147引用：1難度：0.8

  解析

• 2．“x=2kπ+

  π

  6

  ，k∈Z”是“sinx=

  1

  2

  ”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充分必要條件	D．既不充分也不必要條件
  組卷：661引用：7難度：0.9

  解析

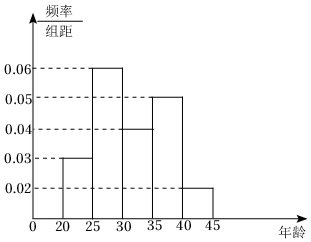• 3．為遏制新型冠狀病毒肺炎疫情的傳播，我市某區對全體居民進行核酸檢測．現面向全區招募1000名志愿者，按年齡分成5組：第一組[20，25），第二組[25，30），第三組[30，35），第四組[35，40），第五組[40，45]，經整理得到如下的頻率分布直方圖．若采用分層抽樣的方法從前三組志愿者中抽出39人負責醫療物資的運輸工作，則在第二組中抽出的人數為（　　）

  A．6

  B．9

  C．12

  D．18
  組卷：275引用：2難度：0.7

  解析

• 4．已知一個圓柱的高是底面半徑的2倍，且其上、下底面的圓周均在球面上，若球的體積為

  32

  π

  3

  ，則圓柱的體積為（　　）

  A．16π

  B．8π

  C． 4 2 π

  D． 2 2 π
  組卷：494引用：3難度：0.6

  解析

• 5．已知拋物線y²=8x的準線與雙曲線

  x

  2

  -

  y

  2

  m

  2

  =

  1

  （

  m

  ＞

  0

  ）

  相交于D、E兩點，且OD⊥OE（O為原點），則雙曲線的漸近線方程為（　　）

  A． y =± 4 3 x

  B． y =± 2 3 3 x

  C． y =± 3 2 x

  D． y =± 15 4 x
  組卷：381引用：2難度：0.7

  解析

• 6．設

  a

  =

  ln

  3

  2

  ，b=0.5^0.8，c=0.8^-0.5，則a、b、c的大小關系為（　　）

  A．c＜b＜a

  B．b＜a＜c

  C．a＜b＜c

  D．c＜a＜b
  組卷：440引用：1難度：0.8

  解析

三、解答題：本大題共5小題，共75分．解答應寫出必要的文字說明、推證過程或演算步驟．

• 19．已知橢圓

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  的右頂點為A，上頂點為B，離心率為

  2

  2

  ，且

  |

  AB

  |

  =

  6

  ．
  （Ⅰ）求橢圓的方程；
  （Ⅱ）過點A的直線與橢圓相交于點

  H

  （

  -

  2

  3

  ，

  4

  3

  ）

  ，與y軸相交于點S，過點S的另一條直線l與橢圓相交于M，N兩點，且△ASM的面積是△HSN面積的

  3

  2

  倍，求直線l的方程．
  組卷：292引用：1難度：0.5

  解析

• 20．已知函數

  f

  （

  x

  ）

  =

  alnx

  +

  3

  2

  x

  2

  -

  （

  a

  +

  3

  ）

  x

  ，a∈R．
  （Ⅰ）若曲線y=f（x）在點（2，f（2））處的切線的斜率為4，求a的值；
  （Ⅱ）當a＞0時，求f（x）的單調區間；
  （Ⅲ）已知f（x）的導函數在區間（1，e）上存在零點．求證：當x∈（1，e）時，

  f

  （

  x

  ）

  ＞

  -

  3

  e

  2

  2

  ．
  組卷：521引用：10難度：0.4

  解析