2023年吉林省吉林市高考數學四調試卷

一、單項選擇題：本大題共8小題，脢小題5分，其40分.在海小題給出的四個選項中，只有一個是符合題目要求.

• 1．已知集合A={x∈N||x|＜2}，B={x|ax-1=0}，若B?A，則實數a=（　　）

  A． 1 2 或1

  B．0或1

  C．1

  D． 1 2
  組卷：400引用：4難度：0.7

  解析

• 2．△ABC中，A（3，2），B（1，1），C（2，3），則AB邊上的高所在的直線方程是（　　）

  A．2x+y-7=0

  B．2x-y-1=0

  C．x+2y-8=0

  D．x-2y+4=0
  組卷：503引用：3難度：0.7

  解析

• 3．已知α，β是兩個不同的平面，則下列命題錯誤的是（　　）

  A．若α∩β=l,A∈α且A∈β，則A∈l

  B．若A，B，C是平面α內不共線三點，A∈β，B∈β，則C?β

  C．若直線a?α，直線b?β，則a與b為異面直線

  D．若A∈α且B∈α，則直線AB?α
  組卷：353引用：4難度：0.7

  解析

• 4．下列說法錯誤的是（　　）

  A．若隨機變量X～N（2，σ2），則 P （ X ≥ 2 ） = 1 2

  B．若隨機變量Y服從兩點分布，且 E （ Y ） = 1 2 ，則D（2Y）=1

  C．若隨機變量Z的分布列為 P （ Z = i ） = i + 2 a ， i = - 1 ， 0 ， 1 ， 2 ，則a=10

  D．若隨機變量 T ～ B （ 8 ， 1 3 ） ，則T的分布列中最大的只有P（T=3）
  組卷：124引用：3難度：0.6

  解析

• 5．設

  p

  =

  1

  e

  ，

  q

  =

  ln

  3

  3

  ，

  r

  =

  6

  -

  ln

  27

  e

  2

  ，則（　　）

  A．p＞q＞r

  B．p＞r＞q

  C．r＞p＞q

  D．r＞q＞p
  組卷：104引用：3難度：0.3

  解析

• 6．點G是△ABC的重心，GB⊥GC，BC=4，則

  CA

  ?

  BA

  =（　　）

  A．32

  B．30

  C．16

  D．14
  組卷：52引用：2難度：0.6

  解析

• 7．在我國古代，楊輝三角（如圖1）是解決很多數學問題的有力工具，從圖1中可以歸納出等式：

  C

  1

  1

  +

  C

  1

  2

  +

  C

  1

  3

  +

  ?

  +

  C

  1

  n

  =

  C

  2

  n

  +

  1

  、類比上述結論，借助楊輝三角解決下述問題：如圖2，該“芻童垛”共2021層，底層如圖3，一邊2023個圓球，另一邊2022個圓球，向上逐層每邊減少1個圓球，頂層堆6個圓球，則此“芻童垛”中圓球的總數為（　　）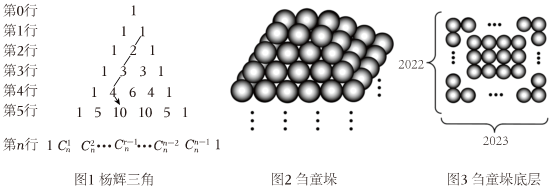
  

  A． 2 C 3 2023 - 2

  B． 2 C 3 2024 - 2

  C． C 4 2024 - 2

  D． C 4 2023 - 2
  組卷：75引用：5難度：0.7

  解析

三、解答題：本大題共6小題，共70分.解答應寫出文字說明，證明過程或演算步驟.

• 21．已知雙曲線C：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =1（a＞0，b＞0）的左、右頂點分別為A（-1，0），B（1，0），動直線l過點M（2，0），當直線l與雙曲線C有且僅有一個公共點時，點B到直線l的距離為

  2

  2

  ．
  （1）求雙曲線C的標準方程；
  （2）當直線l與雙曲線C交于異于A，B的兩點P，Q時，記直線AP的斜率為k₁，直線BQ的斜率為k₂．
  （i）是否存在實數λ，使得k₂=λk₁成立，若存在，求出λ的值；若不存在，請說明理由；
  （ii）求直線AP和BQ交點E的軌跡方程．
  組卷：56引用：1難度：0.5

  解析

• 22．已知函數f（x）=xlnx-m（x-1），且f（x）≥0．
  （1）求實數m的取值范圍；
  （2）設k為整數，且對任意正整數n,不等式

  （

  1

  +

  1

  3

  ）

  （

  1

  +

  1

  3

  2

  ）

  ?

  （

  1

  +

  1

  3

  n

  ）

  ＜

  k

  恒成立，求k的最小值；
  （3）證明：

  （

  2023

  2024

  ）

  2024

  ＜

  1

  e

  ＜

  （

  2023

  2024

  ）

  2023

  ．
  組卷：101引用：3難度：0.3

  解析