當前位置：試卷中心 > 試卷詳情

2022年浙江省9+1高中聯盟高考數學模擬試卷（4月份）

發布：2024/4/20 14:35:0

一、選擇題（本大題共10小題，每小題4分，共40分，在每小題給出的四個選項中，只有一項是符合題目要求的）

1．記A={x|log₂（x-1）＜3}，A∩N=B，則B的元素個數為（　　）
A．6 B．7 C．8 D．9
組卷：46引用：2難度：0.8
解析
2．如圖為陜西博物館收藏的國寶——唐-金筐寶鈿團化紋金杯，杯身曲線內收，玲瓏嬌美，巧奪天工，是唐朝金銀細作的典范之作．該杯的主體部分可以近似看作是雙曲線C：
x
2
a
2
-
y
2
b
2
=1（a＞0，b＞0）的右支與直線x=0，y=6，y=-3圍成的曲邊四邊形ABMN繞y軸旋轉一周得到的幾何體，若該金杯主體部分的上口外直徑為
4
5
，下底外直徑為
26
，則此雙曲線C的離心率為（　　）
A．2 B．
2
C．
3
D．3
組卷：82引用：1難度：0.6
解析
3．在
（
1
x
-
x
2
）
6
的展開式中x⁶的系數是（　　）
A．-20 B．-15 C．20 D．15
組卷：236引用：5難度：0.7
解析
4．函數
y
=
e
x
|
x
|
cos
（
-
x
）
e
2
x
+
1
的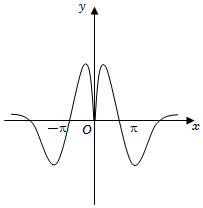部分圖像大致為（　　）
A． B．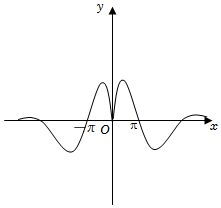
C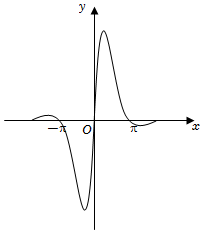． D．
組卷：140引用：1難度：0.7
解析
5．設a,b∈（0，1）∪（1，+∞），則“log_ab=log_ba”是“a=b”的（　　）
A．充分不必要條件 B．必要不充分條件
C．充要條件 D．既不充分也不必要條件
組卷：85引用：3難度：0.9
解析
6．已知實數a,b,c∈（0，e），且2^a=a²，3^b=b³，5^c=c⁵，則（　　）
A．（a-c）（a-b）＜0 B．（c-a）（c-b）＜0
C．（b-a）（b-c）＜0 D．b＜a＜c
組卷：357引用：7難度：0.5
解析
7．已知經過圓柱O₁O₂旋轉軸的給定平面α，A，B是圓柱O₁O₂側面上且不在平面α上的兩點，則下列判斷正確的是（　　）
A．不一定存在直線l,l?α且l與AB異面
B．一定存在直線l,l?α且l⊥AB
C．不一定存在平面β，AB?β且β⊥α
D．一定存在平面β，AB?β且β∥α
組卷：97引用：1難度：0.5
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

三、解答題（本大題共5小題，共74分。解答應寫出文字說明、證明過程或演算步驟）

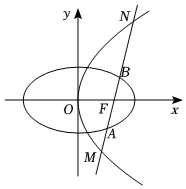21．已知拋物線G：y²=8x的焦點與圓E：
x
2
a
2
+
y
2
b
2
=
1
（
a
＞
b
＞
0
）
的右焦點F重合，橢圓E的短軸長為2．
（1）求橢圓E的方程；
（2）過點F且斜率為k的直線l交橢圓E于A、B兩點，交拋物線G于M，N兩點，請問是否存在實常數t,使
5
|
AB
|
+
t
|
MN
|
為定值？若存在，求出t的值；若不存在，說明理由．
組卷：231引用：3難度：0.5
解析
22．已知
f
（
x
）
=
x
lnx
，
g
（
x
）
=
x
2
+
e
2
2
x
（
x
＞
0
）
，f（x₁）=f（x₂）=g（x₃）=g（x₄）=m（m＞e），1＜x₁＜x₂，0＜x₃＜x₄．
（1）求f（x）的單調區間；
（2）若
G
（
x
）
=
1
f
（
x
）
+
1
x
+
a
（
x
-
1
）
在區間（0，+∞）上單調遞增，求實數a的取值范圍；
（3）求證：x₂+x₃＞x₁+x₄．
組卷：177引用：1難度：0.3
解析