2022-2023學年廣東省佛山市南海外國語學校九年級（上）期中數學試卷

一、選擇題（共10小題，每小題3分，共30分）

• 1．如圖，該幾何體的左視圖為（　　）
  

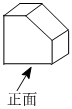
  A．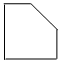

  B．

  C．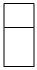

  D．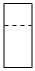
  組卷：19引用：1難度：0.8

  解析

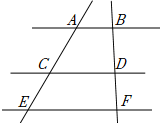• 2．如圖，AB∥CD∥EF，AC：CE=3：2，BD=6，則DF的長為（　　）

  A．2

  B．4

  C．9

  D．10
  組卷：391引用：5難度：0.5

  解析

• 3．一元二次方程2x²-7x-1=0的根的情況是（　　）

  A．有兩個不相等的實數根	B．有兩個相等的實數根
  C．沒有實數根	D．不能確定
  組卷：777引用：12難度：0.8

  解析

• 4．若方程（m-2）

  x

  m

  2

  -

  2

  +3x-2=0是關于x的一元二次方程，則m的值是（　　）

  A．2

  B．-2

  C．±2

  D．0
  組卷：223引用：7難度：0.8

  解析

• 5．在不透明的袋子中裝有黑、白兩種球共50個，這些球除顏色外都相同，隨機從袋中摸出一個球，記錄下顏色后，放回袋子中并搖勻，再從中摸出一個球，經過如此大量重復試驗，發現摸出的黑球的頻率穩定在0.4附近，則袋子中黑球的個數約為（　　）

  A．20個

  B．30個

  C．40個

  D．50個
  組卷：376引用：8難度：0.6

  解析

• 6．某樂器上的一根弦AB=80cm,兩個端點A、B固定在樂器面板上，支撐點C是AB的黃金分割點，且AC＞BC，則AC的長（　　）

  A．40（ 5 - 1 ）cm

  B．40（ 5 +1）cm

  C．40（3- 5 ）cm

  D．40（3+ 5 ）cm
  組卷：250引用：2難度：0.6

  解析

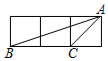• 7．如圖，每個小正方形邊長均為1，則圖中四個陰影的三角形中與△ABC相似的是（　　）

  A．

  B．

  C．

  D．
  組卷：109引用：2難度：0.7

  解析

三、解答題（共8小題，16、17、18題每題8分，19、20、21題每題9分，22、23題每題12分，共75分）

• 22．閱讀材料：把形如x²+bx+c的二次三項式（或其一部分）配成完全平方式的方法叫做配方法，配方法的基本形式是完全平方公式的逆寫，即a²±2ab+b²=（a±b）²．
  例如：x²-2x+4=x²-2x+1+3=（x-1）²+3；
  x²-2x+4=x²-4x+4+2x=（x-2）²+2x；
  x²-2x+4=

  1

  4

  x

  2

  -

  2

  x

  +

  4

  +

  3

  4

  x

  2

  =

  （

  1

  2

  x

  -

  2

  ）

  2

  +

  3

  4

  x

  2

  ；
  是x²-2x+4的三種不同形式的配方（即“余項”分別是常數項、一次項、二次項）．
  請根據閱讀材料解決下列問題：
  （1）比照上面的例子，將二次三項式x²-6x+16配成完全平方式（直接寫出兩種形式）；
  （2）已知a、b、c是△ABC的三邊，且滿足a²+2b²+c²-2b（a+c）=0，試判斷此三角形的形狀并說明理由；
  （3）已知2x+y=6，求當x、y分別取什么值時，x²+2xy+y²-3x-2y取最小值，最小值是多少？
  組卷：81引用：2難度：0.5

  解析

• 23．【感知】
  如圖1，在四邊形ABCD中，點P在邊AB上（不與A、B重合），∠A=∠B=∠DPC=90°．易證：△DAP∽△PBC（不要求證明）．
  【探究】
  如圖2，在四邊形ABCD中，點P在邊AB上（點P不與點A、B重合），∠A=∠B=∠DPC．
  （1）求證：△DAP∽△PBC．
  （2）若PD=5，PC=10，BC=9，則AP的長為

  ．
  【應用】
  如圖3，在△ABC中，AC=BC=8，AB=12．點P在邊AB上（點P不與點A、B重合），連結CP，作∠CPE=∠A，PE與邊BC交于點E．
  （3）當CE=3EB時，求AP的長．
  （4）當△CPE是等腰三角形時，直接寫出AP的長．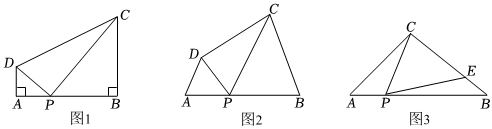
  
  組卷：122引用：2難度：0.5

  解析