2021-2022學(xué)年江西省臨川第一中學(xué)暨臨川一博中學(xué)高一（下）期中數(shù)學(xué)試卷

一、選擇題：本大題共8小題，每小題5分，共40分．在每小題給出的四個(gè)選項(xiàng)中，只有一項(xiàng)是符合題目要求的．

• 1．已知下列三角函數(shù)：①sin2022°；②

  cos

  （

  -

  23

  4

  π

  ）

  ；③cos940°；④sin3，其中值為正的是（　　）

  A．①②

  B．②③

  C．①④

  D．②④
  組卷：19引用：1難度：0.8

  解析

• 2．已知

  a

  =

  sin

  1

  2

  ，

  b

  =

  cos

  π

  6

  ，

  c

  =

  tan

  2

  ，則a、b、c的大小關(guān)系為（　　）

  A．a(chǎn)＜b＜c

  B．a(chǎn)＜c＜b

  C．c＜a＜b

  D．c＜b＜a
  組卷：62引用：3難度：0.7

  解析

• 3．已知M（-2，7），N（10，-2），點(diǎn)P是線段MN上的點(diǎn)，且

  PN

  =-2

  PM

  ，則點(diǎn)P的坐標(biāo)是（　　）

  A．（-14，16）

  B．（22，-11）

  C．（6，1）

  D．（2，4）
  組卷：421引用：21難度：0.9

  解析

• 4．在等腰梯形ABCD中，AB∥DC，AB=2DC，E為BC的中點(diǎn)，則（　　）

  A． AE = 3 4 AB + 1 2 AD	B． AE = 3 2 AB + 1 2 AD
  C． AE = 1 4 AB + 1 2 AD	D． AE = 3 4 AB + 1 4 AD
  組卷：300引用：7難度：0.8

  解析

• 5．下列說(shuō)法正確的是（　　）

  A．與角 19 π 6 終邊相同的角α的集合可以表示為 { α | α = 2 kπ + π 6 ， k ∈ Z }

  B．若α為第一象限角，則 α 2 仍為第一象限角

  C．函數(shù)f（x）=sin（x+φ+ π 4 ）是偶函數(shù)，則φ的一個(gè)可能值為 3 π 4

  D．點(diǎn) （ 7 π 12 ， 0 ） 是函數(shù) f （ x ） = 2 cos （ 2 x + π 3 ） 的一個(gè)對(duì)稱中心
  組卷：196引用：3難度：0.6

  解析

• 6．函數(shù)y=（2^x-2^-x）sinx在[-π，π]的圖象大致為（　　）

  A．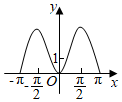

  B．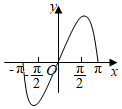

  C．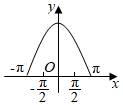

  D．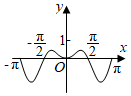
  組卷：255引用：13難度：0.7

  解析

• 7．已知P是邊長(zhǎng)為3的正方形ABCD內(nèi)（包含邊界）的一點(diǎn)，則

  AP

  ?

  AB

  的最大值是（　　）

  A．6

  B．3

  C．9

  D．8
  組卷：70引用：2難度：0.7

  解析

四、解答題：共本大題6小題，共70分．解答應(yīng)寫出必要的文字說(shuō)明、證明過(guò)程及演算步驟．

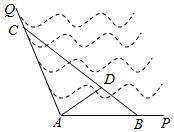• 21．如圖所示，∠PAQ是某海灣旅游區(qū)的一角，其中∠PAQ=120°，為了營(yíng)造更加優(yōu)美的旅游環(huán)境，旅游區(qū)管委員會(huì)決定在直線海岸AP和AQ上分別修建觀光長(zhǎng)廊AB和AC，其中AB是寬長(zhǎng)廊，造價(jià)是800元/米；AC是窄長(zhǎng)廊，造價(jià)是400元/米；兩段長(zhǎng)廊的總造價(jià)為120萬(wàn)元，同時(shí)在線段BC上靠近點(diǎn)B的三等分點(diǎn)D處建一個(gè)觀光平臺(tái)，并建水上直線通道AD（平臺(tái)大小忽略不計(jì)），水上通道的造價(jià)是1000元/米．
  （1）若規(guī)劃在三角形ABC區(qū)域內(nèi)開(kāi)發(fā)水上游樂(lè)項(xiàng)目，要求△ABC的面積最大，那么AB和AC的長(zhǎng)度分別為多少米？
  （2）在（1）的條件下，建直線通道AD還需要多少錢？
  組卷：371引用：9難度：0.3

  解析

• 22．在△ABC中，角A，B，C的對(duì)邊分別為a,b,c,已知asinA+asinCcosB+bsinCcosA=bsinB+csinA
  （1）求角B的大小；
  （2）若

  b

  =

  3

  6

  ，

  c

  =

  3

  2

  ，點(diǎn)D滿足

  AD

  =

  2

  3

  AB

  +

  1

  3

  AC

  ，求△ABD的面積；
  （3）若b²=ac,且外接圓半徑為2，圓心為O，P為⊙O上的一動(dòng)點(diǎn)，試求

  PA

  ?

  PB

  的取值范圍．
  組卷：125引用：6難度：0.4

  解析