2020-2021學年湖南省益陽市桃江一中高二(下)入學數學試卷
發布:2024/4/20 14:35:0
一、單項選擇題(本大題共8小題,每小題5分,共40分).
-
1.命題p:?x0∈[-1,4],f(x0)<0,則?p是( )
A.?x∈[-1,4],f(x)<0 B.?x0∈[-1,4],f(x0)≥0 C.?x0∈[-1,4],f(x0)≤0 D.?x∈[-1,4],f(x)≥0 組卷:4引用:1難度:0.8 -
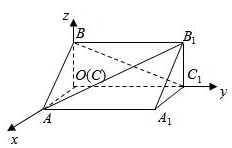 2.如圖,在空間直角坐標系中有直三棱柱ABC-A1B1C1,CA=CC1=2CB,則直線BC1與直線AB1E夾角的余弦值為( )
2.如圖,在空間直角坐標系中有直三棱柱ABC-A1B1C1,CA=CC1=2CB,則直線BC1與直線AB1E夾角的余弦值為( )A. 55B. 52C. 255D. 52組卷:105引用:4難度:0.7 -
3.“m>0且n>0”是“mn>0”成立的( )
A.充分不必要條件 B.必要不充分條件 C.充要條件 D.不充分不必要條件 組卷:2引用:1難度:0.9 -
4.已知x>0,y>0,且
,則3x+4y的最小值是( )35x+15y=1A.5 B.6 C. 285D. 245組卷:617引用:3難度:0.7 -
5.在△ABC中,AD為BC邊上的中線,E為AD的中點,則
=( )EBA. 34-AB14ACB. 14-AB34ACC. 34+AB14ACD. 14+AB34AC組卷:17621引用:169難度:0.9 -
 6.函數f(x)=cos(ωx+φ)(ω>0,|φ|<)的部分圖象如圖所示,則函數f(x)的單調增區間為( )π2
6.函數f(x)=cos(ωx+φ)(ω>0,|φ|<)的部分圖象如圖所示,則函數f(x)的單調增區間為( )π2A.[- +2kπ,11π12+2kπ](k∈Z)π12B.[- +kπ,11π12+kπ](k∈Z)π12C.[- +2kπ,5π12+2kπ](k∈Z)π12D.[- +kπ,5π12+kπ](k∈Z)π12組卷:373引用:6難度:0.7 -
7.若函數f(x)=x-lnx+ex-1+e-x+1+m有零點,則實數m的取值范圍是( )
A.(-∞,-3] B.(-∞,-1] C.[-1,+∞) D.[3,+∞) 組卷:1引用:1難度:0.6
四、解答題(第17題10分,第18-22題每題12分,共70分,解答應寫出文字說明、證明過程或演算步驟)
-
21.已知橢圓M:
+x2a2=1(a>b>0)的離心率為y2b2,且橢圓上一點P的坐標為(32,2).22
(1)求橢圓M的方程;
(2)設直線l與橢圓M交于A,B兩點,且以線段AB為直徑的圓過橢圓的右頂點C,求△ABC面積的最大值.組卷:973引用:4難度:0.4 -
22.已知函數
.f(x)=-alnx+x+1-ax
(1)當a≥2時,求函數f(x)的單調區間;
(2)設g(x)=ex+mx2-3,當a=e2+1時,對任意x1∈[1,+∞),存在x2∈[1,+∞),使,證明:m≤e2-e.f(x1)+2e2≥g(x2)組卷:160引用:2難度:0.3


