2014-2015學年上海市松江二中高二（上）開學數學試卷

一、填空題（每題3分，共36分）

• 1．計算：

  lim

  n

  →∞

  2

  n

  +

  10

  3

  n

  +

  23

  =

  ．
  組卷：23引用：3難度：0.9

  解析

• 2．已知函數f（x）=

  1

  2

  sin（ax+

  2

  π

  7

  ）的最小正周期為4π，則正實數a=

   

  ．
  組卷：18引用：1難度：0.9

  解析

• 3．已知等比數列{a_n}中，a₁+a₂=2，a₃+a₄=4，則a₅+a₆=

  ．
  組卷：316引用：7難度：0.9

  解析

• 4．若等差數列{a_n}的前n項和為S_n，a₂+a₄=14，S₇=70，則數列{a_n}的通項公式為

  ．
  組卷：49引用：5難度：0.7

  解析

• 5．已知

  sinx

  =

  3

  5

  ，

  x

  ∈

  （

  π

  2

  ，

  π

  ）

  ，則x=

  ．（結果用反三角函數表示）
  組卷：156引用：3難度：0.9

  解析

• 6．若

  lim

  n

  →∞

  （1+

  1

  r

  ）ⁿ=0，則實數r的取值范圍是

  ．
  組卷：68引用：1難度：0.5

  解析

• 7．如果f（n）=1+

  1

  2

  +

  1

  3

  +

  1

  4

  +…+

  1

  2

  n

  （n∈N^*），那么f（n+1）-f（n）=

   

  ．
  組卷：51引用：1難度：0.7

  解析

三、解答題：（本大題共5題，滿分48分）

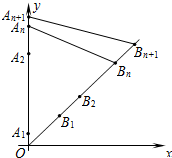• 20．如圖，在y軸的正半軸上依次有點A₁、A₂、…、A_n，其中點A₁（0，1）、A₂（0，10），且|A_n-1A_n|=3|A_nA_n+1|（n=2，3，4，…），在射線y=x（x≥0）上依次有點B₁、B₂、…、B_n，點B₁的坐標為（3，3），且|OB_n|=|OB_n-1|+2

  2

  （n=2，3，4，…）．
  （1）求點A_n、B_n的坐標（用含n的式子表示）；
  （2）設四邊形A_nB_nB_n+1A_n+1面積為S_n，求數列{S_n}的通項公式．
  組卷：55引用：1難度：0.1

  解析

• 21．已知數列{a_n}中，a₁=3，a_n+1+a_n=3?2ⁿ，n∈N^*．
  （1）證明數列{a_n-2ⁿ}是等比數列，并求數列{a_n}的通項公式；
  （2）在數列{a_n}中，是否存在連續三項成等差數列？若存在，求出所有符合條件的項，若不存在，請說明理由；
  （3）已知1＜r＜s且r,s∈N^*，若a₁，a_r，a_s成等差數列，請求出r,s滿足的關系式．
  組卷：110引用：1難度：0.3

  解析