2022-2023學年福建省廈門市思明區松柏中學八年級（下）期末數學試卷

一、選擇題（每小題4分，共40分，每小題都有四個選項，其中有且只有一個選項正確）

• 1．下列二次根式是最簡二次根式的是（　　）

  A． 3

  B． 0 . 25

  C． 1 2

  D． 8
  組卷：50引用：1難度：0.7

  解析

• 2．方程（x-1）（x+2）=0的解是（　　）

  A．x1=1，x2=2	B．x1=-1，x2=2
  C．x1=1，x2=-2	D．x1=-1，x2=-2
  組卷：1062引用：18難度：0.9

  解析

• 3．下列四組數據中，不能作為直角三角形的三邊長的是（　　）

  A．5，12，13

  B．6，8，10

  C． 1 ， 1 ， 2

  D．3，4，6
  組卷：48引用：1難度：0.7

  解析

• 4．若?ABCD對角線AC，BD相交于點O，點E是BC中點，若OE=3，則AB長為（　　）

  A．3

  B．6

  C．9

  D．12
  組卷：56引用：4難度：0.7

  解析

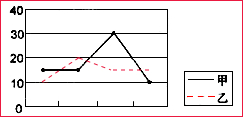• 5．如圖是甲、乙兩組數據的折線統計圖，下列結論中正確的是（　　）

  A．甲組數據比乙組數據穩定

  B．乙組數據比甲組數據穩定

  C．甲、乙兩組數據一樣穩定

  D．不能比較兩組數據的穩定性
  組卷：137引用：15難度：0.9

  解析

• 6．矩形ABCD中，對角線AC，BD交于點O．若∠COB=120°，BD=8，則AB的長為（　　）

  A．4

  B． 4 3

  C．3

  D．5
  組卷：70引用：1難度：0.7

  解析

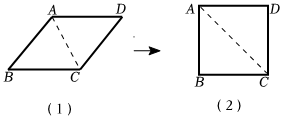• 7．小明用四根長度相等的木條制作了能夠活動的菱形學具，他先活動學具成為圖（1）所示的菱形，并測得∠B=60°，接著活動學具成為圖（2）所示的正方形，并測得對角線AC=20

  2

  ，則圖（1）中菱形的對角線BD長為（　　）

  A．20

  B．30

  C． 20 3

  D． 20 2
  組卷：918引用：10難度：0.5

  解析

• 8．已知一次函數y=kx+b,函數值y隨自變量x的減小而增大，且k+b＞0，則函數y=kx+b的圖象大致是（　　）

  A．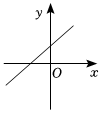

  B．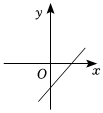

  C．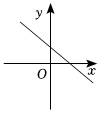

  D．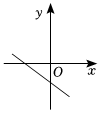
  組卷：186引用：1難度：0.5

  解析

三、解答題（本大題共9個小題，共86分）

• 24．如圖1，在正方形ABCD中，F是BC的中點，連接AF，過點D作DE⊥AF于點G，交AB于點E，過點B作BM⊥AF于點M．
  （1）求證：E為AB的中點；
  （2）求證：AG=GM；
  （3）如圖2，連接DM，作∠CDM的平分線交BC于點N，求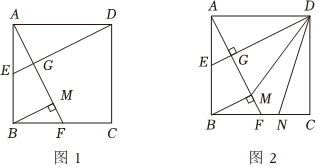

  CN

  DM

  的值．
  
  組卷：104引用：1難度：0.2

  解析

• 25．在平面直角坐標系中，對于任意兩點A（x₁，y₁）和B（x₂，y₂），稱點（x₁x₂，y₁y₂）為點A和B的融合點．如（2，3）和（1，4）的融合點是（2，12）．
  （1）點（3，2）和（0.5，6）的融合點坐標是

  ；
  （2）已知點P（3，1）和直線l：y=-2x+4．設點Q是直線l上任意一點，點P和Q的融合點為點T．
  ①求證：當點Q在直線l上移動時，點T始終在同一條直線上．
  ②若

  M

  （

  -

  1

  ，

  0

  ）

  ，

  N

  （

  0

  ，-

  2

  3

  ）

  ，求△MNT的面積．
  （2）對于點C（m,n）（mn≠0）和直線h：y=kx+b（k≠0），點D是直線h上任意一點，類似（2），可證明當點D在直線h上移動時，點C和D的融合點始終在同一條直線上，稱該直線為點C和直線h的融合直線．已知直線s：y=3x+4，點R在直線x=2上且縱坐標不為0，點R和直線s的融合直線記為t.點E（-2，2）點F（2，-2），若融合直線t與線段EF有公共點，請直接寫出點R的縱坐標y_R的取值范圍．
  組卷：254引用：1難度：0.3

  解析