2022年中學(xué)生標(biāo)準(zhǔn)學(xué)術(shù)能力高考數(shù)學(xué)診斷性試卷（3月份）（新高考卷）

一、單項(xiàng)選擇題：本題共8小題，每小題5分，共40分.在每小題給出的四個(gè)選項(xiàng)中，只有一項(xiàng)是符合題目要求的．

• 1．設(shè)集合A={x|（x+1）（x-1）＜0}，B={y|y＞0}，則A∩（?_RB）=（　　）

  A．?

  B．[0，1）

  C．（-1，0）

  D．（-1，0]
  組卷：35引用：2難度：0.8

  解析

• 2．若復(fù)數(shù)z滿足z（1+i）=2i-1（i為虛數(shù)單位），則下列說(shuō)法正確的是（　　）

  A．z的虛部為 3 2 i

  B．|z|= 10 2

  C．z+ z =3

  D．z在復(fù)平面內(nèi)對(duì)應(yīng)的點(diǎn)在第二象限
  組卷：210引用：4難度：0.7

  解析

• 3．設(shè)a＞0，b＞0，則“9a+b≤4”是“ab≤

  4

  9

  ”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充要條件	D．既不充分也不必要條件
  組卷：39引用：2難度：0.8

  解析

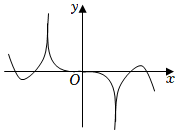• 4．已知函數(shù)f（x）的圖象如圖所示，則該函數(shù)的解析式可能是（　　）

  A．f（x）=ln（1+cosx2）	B．f（x）=x?ln（1-cosx2）
  C．f（x）=ln（1+sinx2）	D．f（x）=x?ln（1-sinx2）
  組卷：76引用：4難度：0.6

  解析

• 5．為了得到函數(shù)y=sin（2x+

  π

  3

  ）的圖象，可以將函數(shù)y=cos（2x+

  π

  4

  ）的圖象（　　）

  A．向左平移 5 π 24 個(gè)單位	B．向右平移 5 π 24 個(gè)單位
  C．向左平移 π 2 個(gè)單位	D．向右平移 π 2 個(gè)單位
  組卷：200引用：3難度：0.7

  解析

• 6．已知α，β，γ是三個(gè)互不相同的銳角，則在sinα+cosβ，sinβ+cosγ，sinγ+cosα三個(gè)值中，大于

  2

  的個(gè)數(shù)最多有（　　）個(gè)

  A．0

  B．1

  C．2

  D．3
  組卷：72引用：1難度：0.6

  解析

• 7．已知橢圓C：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =1（a＞b＞0）的離心率為

  3

  3

  ，過(guò)左焦點(diǎn)F作一條斜率為k（k＞0）的直線，與橢圓交于A，B兩點(diǎn)，滿足|AF|=2|FB|，則實(shí)數(shù)k的值為（　　）

  A．1

  B． 2

  C． 3

  D．2
  組卷：303引用：2難度：0.5

  解析

四、解答題：本題共6小題，共70分.解答應(yīng)寫(xiě)出文字說(shuō)明、證明過(guò)程或演算步驟.

• 21．已知實(shí)數(shù)x,y滿足x²+（e^x-y）²+e^2y=2．
  （1）若x=0時(shí)，試問(wèn)上述關(guān)于y的方程有幾個(gè)實(shí)根？
  （2）證明：使方程x²+（e^x-y）+e^2y=2有解的必要條件為：-2≤x≤0．
  組卷：62引用：2難度：0.6

  解析

• 22．如圖所示，已知拋物線E：y²=2px,其焦點(diǎn)與準(zhǔn)線的距離為6，過(guò)點(diǎn)M（4，0）作直線l₁，l₂與E相交，其中l(wèi)₁與E交于A，B兩點(diǎn)，l₂與E交于C，D兩點(diǎn)，直線AD過(guò)E的焦點(diǎn)F，若AD，BC的斜率為k₁，k₂．
  （1）求拋物線E的方程；
  （2）問(wèn)

  k

  1

  k

  2

  是否為定值？如是，請(qǐng)求出此定值；如不是，請(qǐng)說(shuō)明理由．
  組卷：184引用：3難度：0.5

  解析