當前位置：試卷中心 > 試卷詳情

2022-2023學年重慶市鳳鳴山中學教育集團高三（上）期中數學試卷

發布：2024/4/20 14:35:0

1．已知集合A={x|y=ln（2-x）}，B={y|y=2^x，x∈R}，則A∩B=（　　）
A．[0，1） B．[0，1] C．（0，2） D．（0，2]
組卷：41引用：3難度：0.9
解析
2．在等差數列{a_n}，a₃=
3
2
，a₈=
13
2
，則a₄=（　　）
A．
7
2
B．2 C．
5
2
D．4
組卷：14引用：3難度：0.7
解析
3．已知向量
a
=
（
1
，
-
2
）
，
b
=
（
-
1
，
m
）
，若
a
∥
b
，則m的值為（　　）
A．1 B．-1 C．2 D．-2
組卷：79引用：2難度：0.7
解析
4．甲、乙、丙、丁四人準備從社區組織的道路安全或衛生健康志愿宣傳活動中隨機選擇一個參加，每個人的選擇相互獨立，則甲、乙參加同一個活動的概率為（　　）
A．
1
4
B．
1
3
C．
1
2
D．
3
4
組卷：144引用：2難度：0.7
解析
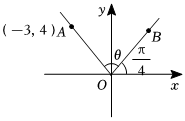5．如圖，在平面直角坐標系xOy中，已知點A（-3，4），
∠
BO
x
=
π
4
，記∠AOB=θ，則sin2θ=（　　）
A．
-
7
25
B．
7
9
C．
-
7
9
D．
7
25
組卷：140引用：3難度：0.8
解析
6．已知定義域為R的偶函數f（x）滿足f（x）+f（4-x）=0，且當x∈[-2，2）時，f（x）=x²-4，則f（2021）=（　　）
A．-3 B．-1 C．1 D．3
組卷：723引用：3難度：0.7
解析
7．若平面向量
a
，
b
，
c
滿足|
c
|=1，
a
?
c
=1，
b
?
c
=3，
a
?
b
=2，則
a
，
b
夾角的取值范圍是（　　）
A．[
π
6
，
π
2
） B．[
π
6
，π） C．[
π
3
，
π
2
） D．[
π
3
，π）
組卷：738引用：4難度：0.3
解析

21．伴隨經濟的飛速發展，中國全民健身賽事活動日益豐富，公共服務體系日趨完善．據相關統計數據顯示，中國經常參與體育鍛煉的人數比例為37.2%，城鄉居民達到《國民體質測定標準》合格以上的人數比例達到90%以上．健身之于個人是一種自然而然的習慣，之于國家與民族，則是全民健康的基礎柱石之一，某市一健身連鎖機構對去年的參與了該連鎖機構健身的會員進行了統計，制作成如下兩個統計圖，圖1為該健身連鎖機構會員年齡等級分布圖，圖2為一個月內會員到健身連鎖機構頻數分布扇形圖．

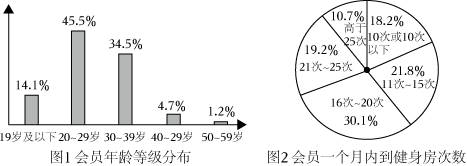
若將會員按年齡分為“年輕人”（20歲-39歲）和“非年輕人”（19歲及以下或40歲及以上）兩類，將一月內來健身房鍛煉16次及以上的會員稱為“健身達人”，15次及以下的會員稱為“健身愛好者”，且已知在“健身達人”中有
5
6
是“年輕人”．
（1）現從該健身連鎖機構會員中隨機抽取一個容量為100人的樣本，根據如圖的數據，補全下方2×2列聯表，并判斷依據小概率值α=0.05的獨立性檢驗，能否認為是否為“健身達人”與年齡有關；

類別年輕人非年輕人合計

健身達人

健身愛好者

合計 100

臨界值表：

ρ（K²＜k₀） 0.40 0.25 0.05 0.005

k₀ 0.708 1.323 3.841 7.879

K
2
=
n
（
ad
-
bc
）
2
（
a
+
b
）
（
c
+
d
）
（
a
+
c
）
（
b
+
d
）

（2）將（1）中的頻率作為概率，連鎖機構隨機選取會員進行回訪，抽取3人回訪．
①若選到的3人中2人為“年輕人”，1人為“非年輕人”，再從這3人中隨機選取的1人，了解到該會員是“健身達人”，求該人為非年輕人的概率；
②設3人中既是“年輕人”又是“健身達人”的人數為隨機變量X，求X的分布列和期望值．

組卷：42引用：2難度：0.6