當前位置：試卷中心 > 試卷詳情

2015年安徽省蚌埠市“成功杯”數學競賽試卷

發布：2024/12/13 2:30:1

1．設1≤x≤3，則|x-1|-|x-3|的最大值與最小值的和是（　　）
A．-1 B．0 C．2 D．3
組卷：666引用：2難度：0.9
解析
2．滿足
（
2
-
x
）
x
2
-
x
-
2
=
1
的所有實數x的和為（　　）
A．3 B．4 C．5 D．6
組卷：556引用：8難度：0.8
解析
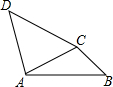3．如圖，在四邊形ABCD中，已知∠ACB=∠BAD=105°，∠ABC=∠ADC=45°，則∠CAD的度數為（　　）
A．60° B．70° C．75° D．80°
組卷：115引用：2難度：0.7
解析
4．已知
x
-
2010
x
=
5
，則
（
x
-
2
）
3
-
（
x
-
1
）
2
+
1
x
-
2
=（　　）
A．2010 B．2012 C．2014 D．2016
組卷：75引用：1難度：0.7
解析
5．設[x]表示不超過實數x的最大整數．若實數a滿足a-
4
a
+
3
a
（
a
-
2
）
a
=
2
，則[a]=（　　）
A．0或2 B．-1或2 C．0或3 D．-3或2
組卷：150引用：1難度：0.7
解析
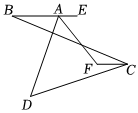6．如圖，平面內有四條線段AB、BC、CD、DA首尾順次相接，點E在BA的延長線上，∠DAE的角平分線與∠BCD的角平分線交于點F．若∠B=26°，∠D=62°，則∠AFC=（　　）
A．131° B．132° C．133° D．134°
組卷：78引用：1難度：0.6
解析

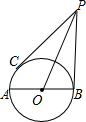19．如圖，已知點C在以AB為直徑的⊙O上，過點B、C作⊙O的切線，且交于點P，連接AC，若OP=
9
2
AC．求
PB
AC
的值．
組卷：245引用：2難度：0.3
解析
20．如果將正整數M放在正整數m左側，所得到的新數可被7整除，那么稱M為m的“魔術數”（例如，把86放在415的左側，得到的數86415能被7整除，所以稱86為415的魔術數）．求正整數n的最小值，使得存在互不相同的正整數a₁，a₂，…，a_n，滿足對任意一個正整數m,在a₁，a₂，…，a_n中都至少有一個為m的魔術數．
組卷：281引用：3難度：0.5
解析