2021-2022學年河南省商丘市夏邑縣八年級（下）期末數學試卷
發布：2024/6/30 8:0:9
一、選擇題（每小題3分，共30分）下列各小題均有四個答案，其中只有一個是正確的。
-
1．函數
中自變量x的取值范圍是（ ）y=2x+1組卷：588引用：12難度：0.9 -
2．下列關于平行四邊形的說法：①平行四邊形的對角相等，鄰角互補；②平行四邊形既是中心對稱圖形，又是軸對稱圖形；③通過平行四邊形對稱中心的任意一條直線可以把平行四邊形的面積等分；④平行四邊形的兩條對角線把平行四邊形的面積四等分．其中錯誤的個數（ ）
組卷：17引用：2難度：0.7 -
3．數學老師計算同學們一學期的數學平均成績時，將平時、期中、期末成績按2：3：5的權重計算，若計算結果不是整數的按四舍五入保留整數．小華平時、期中、期末的數學成績分別為90分、82分、85分，則小華這一學期的數學平均成績（ ）
組卷：1引用：2難度：0.5 -
4．已知某新型感冒病毒的直徑約為0.000000823米，將0.000000823用科學記數法表示（ ）
組卷：230引用：6難度：0.9 -
5．將x、y的值同時擴大到原來的10倍，則關于分式
的值，說法正確的是（ ）x+yxy組卷：24引用：3難度：0.5 -
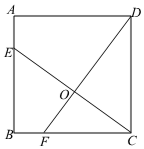6．如圖，點E是正方形ABCD的邊AB上任一點（不與頂點A、B重合），連結CE，過點D作DF⊥CE交BC于F，CE與DF交于點O．則下列說法：①△CBE≌△DCF；②AE=BF；③S四邊形BFOE=S△COD；④S四邊形ABFD=S四邊形ADCE；⑤OE=OC．其中正確的個數是（ ）組卷：9引用：2難度：0.6 -
7．若點P（1-2t,t-3）位于第三象限，則t的取值范圍是（ ）
組卷：11引用：2難度：0.5
-
22．實踐與探究題
問題：直角三角形除了三邊之間、兩個銳角之間有特殊的關系外，斜邊上的中線有什么性質呢？
麗麗同學利用直角三角形紙片進行了如下的折疊實驗：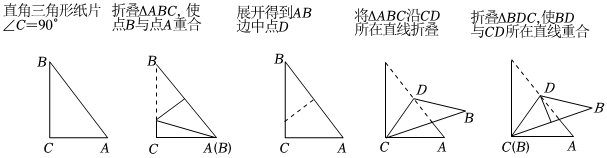
（1）觀察發現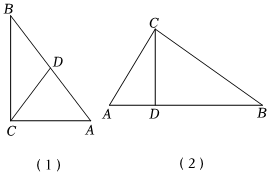
①觀察麗麗同學的折疊實驗，你發現線段CD與AB之間有何數量關系？在圖（1）所示的Rt△ABC中，∠C=90°，CD是斜邊AB上中線．請根據圖（1）證明你的猜想．
②根據上面的探究，總結直角三角形斜邊上的中線性質．
（2）拓展應用：如圖（2），CD是Rt△ABC的斜邊AB上的高，若CD=5，則Rt△ABC面積的最小值等于 ．組卷：193引用：4難度：0.5 -
23．閱讀理解題．
先閱讀下列內容，再完成后面的任務．
在數學探究課上，張老師出示了如下題目：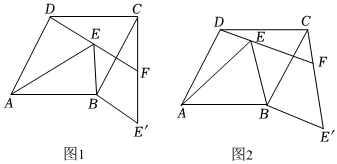
（1）問題1、如圖1，四邊形ABCD是菱形，∠DAB=60°，點E是菱形內的一動點，且∠AEB=60°，將△ABE繞點B順時針旋轉120°得到△CBE'，連接DE，并延長DE交CE'于F．如果∠ABE=90°，猜想四邊形BE'FE為何特殊的平行四邊形？并說明理由．
在同學們順利地解答了問題1后，張老師又將該題做了如下的引申拓展：
（2）問題2、若問題1去掉條件“∠ABE=90°”，其它條件不變，如圖2，上面結論是否還成立？若成立，請證明；若不成立，請說明理由．
經過同學們自探后，“追夢組”的同學們進行了討論；
小菡：沒有了∠ABE=90°這一條件了，應該上面的結論不成立了．
迎暉：觀察圖（2），猜想上面的結論還成立．
夏梅：上面的結論還成立，證明該結論成立的難點是如何證明∠BEF=60°．
迎暉：只要證明了∠AED=60°，就容易證得∠BEF=60°．后面的證明方法與問題1里的證明方法完全一樣了．
……
突然，智明同學說我會證明了：連接BD，在線段AE上截取AH=BE，連接DH，就可以證得∠AED=60°．組里的同學們在智明的啟發下，也順利的解答問題2．
任務一：完整寫出問題1的解答過程；
任務二：在問題2中證明∠BEF=60°（后面的證明不用寫出來了！）．組卷：44引用：2難度：0.5