當前位置：試卷中心 > 試卷詳情

2021-2022學年遼寧省協作校高一（下）期末數學試卷

發布：2024/11/13 15:0:2

一、單項選擇題（本題共8小題，每小題5分，共40分，每小題只有一個選項符合要求）

1．已知復數z滿足z（1-i）=3+i,則復數z的虛部為（　　）
A．-2i B．2i C．-2 D．2
組卷：49引用：5難度：0.8
解析
2．已知2弧度圓心角所對的弦長為2，則這個圓心角所對的弧長為（　　）
A．2sin1 B．sin2 C．
2
sin
1
D．
1
sin
1
組卷：436引用：1難度：0.9
解析
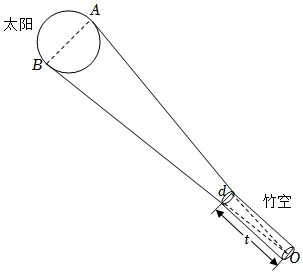3．《周髀算經》中“側影探日行”一文有記載：“即取竹空，徑一寸，長八尺，捕影而視之，空正掩目，而日應空之孔．”意謂：“取竹空這一望筒，當望筒直徑d是一寸，筒長l是八尺時（注：一尺等于十寸），從筒中搜捕太陽的邊緣觀察，則筒的內孔正好覆蓋太陽，而太陽的外緣恰好填滿竹管的內孔．”如圖所示，O為竹空底面圓心，則太陽角∠AOB的正切值為（　　）
A．
320
160
2
-
1
B．
1
160
C．
160
80
2
-
1
D．
1
80
組卷：569引用：12難度：0.5
解析
4．若向量
a
，
b
滿足
a
=（1，0），
b
=（1，
3
），則
b
在
a
上的投影向量為（　　）
A．-
1
4
a
B．
1
4
a
C．-
a
D．
a
組卷：553引用：5難度：0.7
解析
5．數學家歐拉發現了復指數函數和三角函數的關系，并給出以下公式e^ix=cosx+isinx,（其中i是虛數單位，e是自然對數的底數，x∈R），這個公式在復變論中有非常重要的地位，被稱為“數學中的天橋”，根據此公式，有下列四個結論，其中正確的是（　　）
A．e^iπ-1=0 B．2cosx=e^-ix+e^ix
C．2sinx=e^ix-e^-ix D．
（
2
2
+
2
2
i
）
2022
=
-
1
組卷：75引用：1難度：0.5
解析

6．下列命題中正確的是（　　）

A．有一個面是多邊形，其余各面是三角形的幾何體是棱錐

B．有兩個面平行且相似，其余各面都是梯形的多面體是棱臺

C．長方體是正四棱柱

D．四個面都是等邊三角形的四面體是正四面體

組卷：375引用：1難度：0.8

解析

7．已知函數
f
（
x
）
=
3
sin
（
ωx
+
φ
）
（
ω
＞
0
）
，f（x）圖象上每一點橫坐標伸長到原來的2倍，得到g（x）的圖象，g（x）的部分圖象如圖所示，若
AB
?
BC
=
|
AB
|
2
，則w等于（　　）
A．π B．
π
3
C．
π
6
D．
π
12
組卷：153引用：1難度：0.6
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、解答題（本題共6小題，共70分。解答應寫出文字說明、證明過程或演算步驟）

21．如圖1，在直角梯形ABCD中，AB∥CD，∠B=90°，AB=3，CD=2，E在AB上，且△ADE為邊長為2的等邊三角形．將△ADE沿DE折起，使得點A到點P的位置，平面PDE⊥平面BCDE，如圖2．

（1）若F為PC的中點，證明BF∥平面PDE；
（2）證明：PB=PC；
（3）求直線BP與平面DCBE所成角的大小．
組卷：141引用：1難度：0.6
解析
22．已知直三棱柱ABC-A₁B₁C₁中，側面AA₁B₁B為正方形，AB=BC=2，E，F分別為AC和CC₁的中點，D為棱A₁B₁上的點（包括端點）．BF⊥B₁E，若平面A₁B₁E與棱BC交于點G．
（1）試在圖中作出平面A₁B₁E與該棱柱的面相交所得的交線，并指出點G的位置（指出位置即可，不要求過程）；
（2）求證：BF⊥平面A₁B₁E；
（3）當點D運動時，試判斷三棱錐D-EFG的體積是否為定值？若是，求出該定值及點D到平面EFG的距離；若不是，說明理由．
組卷：351引用：5難度：0.5
解析