2021-2022學年北京理工大學附中九年級(下)限時練習數學試卷(5)
發布:2024/4/20 14:35:0
一.選擇題。(共8小題,滿分16分)
-
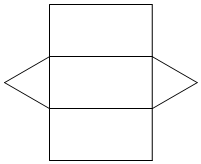 1.如圖是由下列哪個立體圖形展開得到的?( )
1.如圖是由下列哪個立體圖形展開得到的?( )A.圓柱 B.三棱錐 C.三棱柱 D.四棱柱 組卷:385引用:6難度:0.9 -
2.在倡導綠色低碳理念下,兩座公園為迎接2022年北京冬奧會,各準備一個大型的奧運五環,已知每個奧運五環中的單獨圓環所用環保材料的價格為7420000元,那么制作一個奧運五環的價格為( )
A.3.71×107元 B.7.42×106元 C.7.42×107元 D.3.71×106元 組卷:49引用:1難度:0.9 -
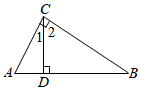 3.如圖已知AC⊥BC,∠A+∠1=90°,則∠2與∠A的關系是( )
3.如圖已知AC⊥BC,∠A+∠1=90°,則∠2與∠A的關系是( )A.∠2大 B.∠A大 C.相等 D.無法確定 組卷:363引用:5難度:0.6 -
4.在平面直角坐標系xOy中,對于點P(a,b),若ab>0,則稱點P為“同號點”.下列函數的圖象中不存在“同號點”的是( )
A.y=-x+1 B.y=x2-2x C.y=- 2xD.y=x2+ 1x組卷:922引用:8難度:0.5 -
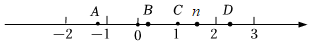 5.已知實數n在數軸對應點的位置如圖所示,實數m滿足.則實數m在數軸上所對應的點n+1m>0,|m|>|n|
5.已知實數n在數軸對應點的位置如圖所示,實數m滿足.則實數m在數軸上所對應的點n+1m>0,|m|>|n|
為( )A.點A B.點B C.點C D.點D 組卷:19引用:1難度:0.8 -
6.在一個不透明紙箱中放有除了數字不同外,其它完全相同的2張卡片,分別標有數字1、2,從中任意摸出一張,放回攪勻后再任意摸出一張,兩次摸出的數字之和為奇數的概率為( )
A. 14B. 13C. 12D. 34組卷:1029引用:12難度:0.5 -
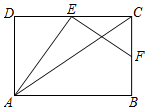 7.如圖,矩形ABCD中,E,F分別為CD,BC的中點,且AE⊥EF,BC=2,則AC的長為( )
7.如圖,矩形ABCD中,E,F分別為CD,BC的中點,且AE⊥EF,BC=2,則AC的長為( )A. 15B.2 2C.3 D.2 3組卷:523引用:6難度:0.6 -
8.某公司生產的一種產品按照質量由高到低分為A,B,C,D四級,為了增加產量、提高質量,該公司改進了一次生產工藝,使得生產總量增加了一倍.為了解新生產工藝的效果,對改進生產工藝前、后的四級產品的占比情況進行了統計,繪制了如下扇形圖:
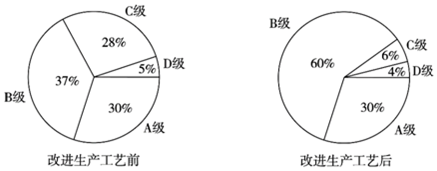
根據以上信息,下列推斷合理的是( )A.改進生產工藝后,A級產品的數量沒有變化 B.改進生產工藝后,B級產品的數量增加了不到一倍 C.改進生產工藝后,C級產品的數量減少 D.改進生產工藝后,D級產品的數量減少 組卷:1162引用:12難度:0.5
二.填空題。(共8小題,滿分16分)
-
9.二次根式
有意義,則x的取值范圍是 .9-3x組卷:1260引用:20難度:0.8
三.解答題。(共68分,第17-20題,每題5分,第21-22題,每題6分,第23題5分,第24題6分,第25題5分,第26題6分,第27-28題,每題7分)
-
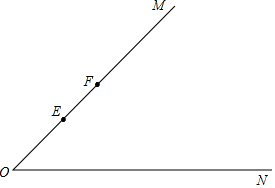 27.如圖,已知∠MON=45°,EF為射線OM上一長度為定值的動線段(點E不與點O重合),EF的垂直平分線交射線ON于點A,交射線OM于點D,連接AF,過點E作AF的垂線,垂足為B,延長BE交ON的反向延長線于點C.
27.如圖,已知∠MON=45°,EF為射線OM上一長度為定值的動線段(點E不與點O重合),EF的垂直平分線交射線ON于點A,交射線OM于點D,連接AF,過點E作AF的垂線,垂足為B,延長BE交ON的反向延長線于點C.
(1)依題意補全圖形,證明:EC=AF;
(2)用等式表示線段OC,OA和OF的關系,并證明;
(3)若EF=4,作∠DBG=45°,G在射線ON上,在線段EF的運動過程中,判斷GB-GO是否為定值,若是,直接寫出該定值,若不是,說明理由.組卷:362引用:3難度:0.1 -
28.在平面直角坐標系xOy中,對于線段MN及點P、Q,若∠MPN=60°且線段MN關于點P的中心對稱線段M'N'恰好經過點Q,則稱點Q是點P的線段MN-60°對經點.
(1)設點A(0,2).
①Q1(2,1),Q2(4,0),Q3(3,-433),其中為某點P的線段OA-60°對經點的是 .12
②已知B(0,1),設⊙B的半徑為r,若⊙B上存在某點P的線段OA-60°對經點,求r的取值范圍;
(2)若點Q(4,0)同時是相異兩點P1、P2的線段OD-60°對經點,直接寫出線段OD長的取值范圍.組卷:163引用:2難度:0.3


