2022-2023學年山東省煙臺市招遠市六年級（下）期中數學試卷（五四學制）

一．選擇題（本大題共10個小題，每小題3分，滿分30分）

• 1．下列四個生產生活現象，可以用“兩點之間線段最短”來解釋的是（　　）

  A．用兩顆釘子可以把木條固定在墻上

  B．在高速公路的建設中，通常從大山中開挖隧道穿過，把道路取直，以縮短路程

  C．植樹時，只要定出兩棵樹的位置，就能使同一行樹坑在一條直線上

  D．打靶的時候，眼睛要與槍上的準星、靶心在同一直線上
  組卷：911引用：9難度：0.8

  解析

• 2．下列計算錯誤的有（　　）
  ①（3xy²）³=27x³y⁶；
  ②（-a^2m）³=a^6m；
  ③x¹²÷x⁴=x³；
  ④2x³?3x⁴=6x¹²．

  A．1個

  B．2個

  C．3個

  D．4個
  組卷：656引用：2難度：0.5

  解析

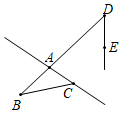• 3．如圖，下列說法中正確的是（　　）

  A．直線AC在線段BC上

  B．射線DE與直線AC沒有公共點

  C．直線AC與線段BD相交于點A

  D．點D在直線AC上
  組卷：204引用：2難度：0.8

  解析

• 4．在下列多項式乘法中，可以用平方差公式計算的是（　　）

  A．（-2a+3b）（-3b-2a）	B．（2a-3b）（-2a+3b）
  C．（a+1）（-a-1）	D．（a2-b）（a+b2）
  組卷：235引用：2難度：0.5

  解析

• 5．已知本學期某學校下午上課的時間為14時20分，則此時刻鐘表上的時針與分針的夾角為_____度．（　　）

  A．40°

  B．50°

  C．60°

  D．70°
  組卷：267引用：3難度：0.6

  解析

• 6．如果多項式4x²-（a-1）x+9是一個完全平方式，則a的值是（　　）

  A．±6

  B．7或-5

  C．13或-11

  D．±12
  組卷：970引用：4難度：0.5

  解析

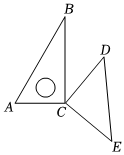• 7．如圖，是直角頂點重合的一副三角板，若∠BCD=40°，下列結論錯誤的是（　　）

  A．∠ACD=130°	B．∠ACD=∠BCE
  C．∠ACE=130°	D．∠ACE-∠BCD=100°
  組卷：594引用：6難度：0.5

  解析

• 8．若a=0.4²，b=-4^-2，

  c

  =

  （

  -

  1

  4

  ）

  -

  2

  ，

  d

  =

  （

  -

  1

  4

  ）

  0

  ，則（　　）

  A．b＜a＜c＜d

  B．b＜a＜d＜c

  C．c＜d＜a＜b

  D．c＜a＜d＜b
  組卷：1096引用：4難度：0.5

  解析

三．解答題（本大題共9個小題，共72分，請在答題卡指定區域做題）

• 24．代數推理：
  

  例題：求x2+8x+21的最小值． 解：x2+8x+21 =x2+2x?4+42-42+21 =（x+4）2+5． 無論x取何值，（x+4）2總是非負數， 即（x+4）2≥0， 所以（x+4）2+5≥5． 所以當x=-4時，x2+8x+21有最小值，最小值為5．

  閱讀材料：利用完全平方式，將多項式x²+bx+c變形為（x+m）²+n的形式，然后由（x+m）²≥0就可以求出多項式x²+bx+c的最小值．
  根據上述材料，解答下列問題：
  （1）填空：x²-12x+

  =（x-

  ）²；
  （2）將多項式x²+16x-1變形為（x+m）²+n的形式，并求出x²+16x-1的最小值；
  （3）若一個長方形的長和寬分別為（2a+3）和（3a+5），面積記為S₁，另一個長方形的長和寬分別為5a和（a+3），面積記為S₂，試比較S₁和S₂的大小，并說明理由．
  組卷：703引用：8難度：0.5

  解析

• 25．學習材料：
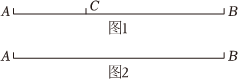
  如圖1，點C在線段AB上，圖中有三條線段，分別為線段AB，AC和BC，若其中一條線段的長度是另外一條線段長度的2倍，則稱點C是線段AB的“巧點”．
  解決問題：
  （1）線段的中點

  這條線段的“巧點”，線段的三等分點

  這條線段的“巧點”（填“是”或“不是”）；
  （2）若線段AB=18cm,點C為線段AB的“巧點”，則AC=

  ；
  （3）如圖2，已知AB=18cm,動點P從點A出發，以2cm/s的速度沿AB向點B運動，點Q從點B出發，以1cm/s的速度沿BA向點A運動，點P、Q同時出發，當其中一點到達終點時，運動停止，設運動的時間為t秒，當t為何值時，點P為線段AQ的“巧點”？并說明理由．
  組卷：268引用：3難度：0.5

  解析