當前位置：試卷中心 > 試卷詳情

2023年廣東省韶關市高考數學二模試卷

發布：2024/4/20 14:35:0

一、選擇題：本題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的．

1．設i為虛數單位，i（1-z）=1，則|z|=（　　）
A．1 B．
2
C．
3
D．2
組卷：149引用：5難度：0.7
解析
2．若集合
M
=
{
x
|
x
＞
1
}
，
N
=
{
x
|
y
=
ln
（
3
2
-
x
）
}
，則M∩N=（　　）
A．{x|0≤x＜2} B．
{
x
|
1
＜
x
＜
3
2
}
C．
{
x
|
1
≤
x
＜
3
2
}
D．
{
x
|
1
＜
x
≤
3
2
}
組卷：87引用：2難度：0.8
解析
3．已知ABCD是平行四邊形，
AE
=
2
EB
，若
EC
=
λ
AB
+
μ
AD
，則λ+μ=（　　）
A．
2
3
B．1 C．
4
3
D．
3
2
組卷：166引用：4難度：0.9
解析
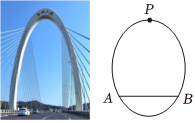4．韶州大橋是一座獨塔雙索面鋼砼混合梁斜拉橋，具有樁深，塔高、梁重、跨大的特點，它打通了曲江區、湞江區、武江區交通道路的瓶頸，成為連接曲江區與芙蓉新城的重要交通橋梁，大橋承擔著實現韶關“三區融合”的重要使命，韶州大橋的橋塔外形近似橢圓，若橋塔所在平面截橋面為線段AB，且AB過橢圓的下焦點，AB=44米，橋塔最高點P距橋面110米，則此橢圓的離心率為（　　）
A．
1
3
B．
2
5
C．
2
3
D．
4
5
組卷：62引用：2難度：0.5
解析
5．已知四棱臺ABCD-A₁B₁C₁D₁的下底面為矩形，AB=2A₁B₁，高為3，且該棱臺的體積為63，則該棱臺上底面A₁B₁C₁D₁的周長的最小值是（　　）
A．15 B．14 C．13 D．12
組卷：84引用：2難度：0.6
解析
6．函數
f
（
x
）
=
A
sin
（
ωx
+
φ
）
（
A
＞
0
，
ω
＞
0
，
|
φ
|
＜
π
2
）
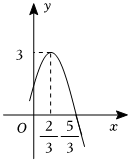的部分圖象如圖所示，將函數f（x）圖象上所有點的橫坐標變為原來的
ω
2
（縱坐標不變），再向左平移
π
12
個單位得到y=g（x）的圖象，則下列說法不正確的是（　　）
A．函數g（x）的最小正周期為π
B．函數g（x）在
[
0
，
π
2
]
上單調遞增
C．函數g（x）的一個極值點為
π
12
D．函數g（x）的一個零點為
-
π
6
組卷：134引用：2難度：0.6
解析
7．已知方程x+5+lnx=0和x+5+e^x=0的解分別是α和β，則函數f（x）=（x+α）（x+β）的單調遞減區間是（　　）
A．
（
-
∞
，
5
2
]
B．
[
5
2
，
+
∞
）
C．（-∞，5] D．[5，+∞）
組卷：60引用：3難度：0.6
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、解答題：本題共6小題，共70分．解答應寫出文字說明、證明過程或演算步驟．

21．已知雙曲線C：
x
2
a
2
-
y
2
b
2
=
1
（
b
＞
0
）
的左右焦點為F₁，F₂，經過F的圓O（O為坐標原點）交雙曲線C的左支于M，N，且△OMN為正三角形．
（1）求雙曲線C的標準方程及漸近線方程；
（2）若點P為雙曲線C右支上一點，射線PF₁，PF₂分別交雙曲線C于點A，B，試探究
|
P
F
1
|
|
A
F
1
|
-
|
P
F
2
|
|
B
F
2
|
是否為定值？若是，求出該定值；若不是，請說明理由．
組卷：84引用：2難度：0.5
解析
22．已知f（x）=sinx,g（x）=x-m,m∈R．
（1）求曲線y=f（x）在點
（
π
3
，
3
2
）
處的切線與兩坐標軸所圍成的三角形的面積；
（2）若h（x）=f（x）?g（x），
x
∈
（
-
π
2
，
+
∞
）
，設x₁，x₂，x₃，…，x_n（其中x_n＜x_n+1，n∈N^*）為h（x）的極值點，若h（x₁）+h（x₂）=0，求m的值．
組卷：41引用：2難度：0.6
解析

0/60 進入組卷

0/20 進入試卷籃

布置作業 發布測評 反向細目表 平行組卷 下載答題卡 試卷分析 在線訓練 收藏試卷

充值會員，資源免費下載

2023年廣東省韶關市高考數學二模試卷

一、選擇題：本題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的．

1．設i為虛數單位，i（1-z）=1，則|z|=（ ）

2．若集合M={x|x＞1}，N={x|y=ln（32-x）}，則M∩N=（ ）

3．已知ABCD是平行四邊形，AE=2EB，若EC=λAB+μAD，則λ+μ=（ ）

5．已知四棱臺ABCD-A1B1C1D1的下底面為矩形，AB=2A1B1，高為3，且該棱臺的體積為63，則該棱臺上底面A1B1C1D1的周長的最小值是（ ）

6．函數f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜π2）的部分圖象如圖所示，將函數f（x）圖象上所有點的橫坐標變為原來的ω2（縱坐標不變），再向左平移π12個單位得到y=g（x）的圖象，則下列說法不正確的是（ ）

7．已知方程x+5+lnx=0和x+5+ex=0的解分別是α和β，則函數f（x）=（x+α）（x+β）的單調遞減區間是（ ）

四、解答題：本題共6小題，共70分．解答應寫出文字說明、證明過程或演算步驟．

1．設i為虛數單位，i（1-z）=1，則|z|=（　　）

2．若集合
M
=
{
x
|
x
＞
1
}
，
N
=
{
x
|
y
=
ln
（
3
2
-
x
）
}
，則M∩N=（　　）

3．已知ABCD是平行四邊形，
AE
=
2
EB
，若
EC
=
λ
AB
+
μ
AD
，則λ+μ=（　　）

5．已知四棱臺ABCD-A₁B₁C₁D₁的下底面為矩形，AB=2A₁B₁，高為3，且該棱臺的體積為63，則該棱臺上底面A₁B₁C₁D₁的周長的最小值是（　　）

7．已知方程x+5+lnx=0和x+5+e^x=0的解分別是α和β，則函數f（x）=（x+α）（x+β）的單調遞減區間是（　　）