當(dāng)前位置：試卷中心 > 試卷詳情

2022-2023學(xué)年河北省邯鄲市叢臺(tái)區(qū)錦玉中學(xué)八年級(jí)（上）期末數(shù)學(xué)試卷

發(fā)布：2024/4/20 14:35:0

一、選擇題（本大題共16小題，1-10題每小題3分，11-16題每小題3分，共42分）

1．下列圖案中，是軸對(duì)稱圖形的是（　　）
A． B． C． D．
組卷：52引用：2難度：0.9
解析
2．下列四個(gè)圖形中，線段BD是△ABC的高的是（　　）
A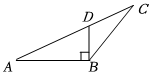． B．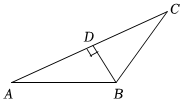
C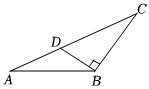． D．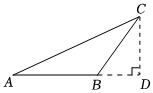
組卷：211引用：4難度：0.7
解析
3．如果一個(gè)多邊形的每一個(gè)外角都等于60°，這個(gè)多邊形的邊數(shù)是（　　）
A．4 B．5 C．6 D．7
組卷：75引用：6難度：0.9
解析
4．若分式
3
x
-
5
有意義，則x的取值范圍是（　　）
A．x≠3 B．x≠5 C．x＞5 D．x＞-5
組卷：60引用：1難度：0.7
解析
5．在平面直角坐標(biāo)系中，點(diǎn)P（1，-3）關(guān)于x軸的對(duì)稱點(diǎn)坐標(biāo)是（　　）
A．（1，-3） B．（-1，3） C．（-1，-3） D．（1，3）
組卷：72引用：7難度：0.9
解析
6．下列由左到右的變形，屬于因式分解的是（　　）
A．m（x+y）=mx+my B．x²-4+3x=（x+2）（x-2）+3
C．（x+3）（x-3）=x²-9 D．x³-x=x（x+1）（x-1）
組卷：103引用：2難度：0.8
解析
7．下列各式
3
a
，
a
+
b
7
，
1
x
-
1
，
x
8
π
，
1
x
2
-
x
中，分式有（　　）個(gè)．
A．1個(gè) B．2個(gè) C．3個(gè) D．4個(gè)
組卷：289引用：1難度：0.8
解析
8．已知a≠0，下列運(yùn)算中正確的是（　　）
A．a(chǎn)²?a³=a⁶ B．a(chǎn)⁵-a³=a² C．（-a³）²=a⁵ D．a(chǎn)?a³=a⁴
組卷：325引用：2難度：0.8
解析

當(dāng)前模式為游客模式，立即登錄查看試卷全部?jī)?nèi)容及下載

三、解答題（本大題共7小題，共68分）

25．閱讀材料：我們把多項(xiàng)式a²+2ab+b²及a²-2ab+b²叫做完全平方式．如果一個(gè)多項(xiàng)式不是完全平方式，我們常做如下變形：先添加一個(gè)適當(dāng)?shù)捻?xiàng)，使式子中出現(xiàn)完全平方式，再減去這個(gè)項(xiàng)，使整個(gè)式子的值不變，這種方法叫做配方法．配方法是一種重要的解決問題的數(shù)學(xué)方法，不僅可以將一個(gè)看似不能分解的多項(xiàng)式分解因式，還能解決一些與非負(fù)數(shù)有關(guān)的問題或求代數(shù)式的最大值，最小值等．例分解因式：x²+2x-3=（x²+2x+1）-4=（x+1）²-4=（x+1+2）（x+1-2）=（x+3）（x-1）；又例如：求代數(shù)式2x²+4x-6的最小值：∵2x²+4x-6=2（x²+2x-3）=2（x+1）²-8；又∵（x+1）²≥0；∴當(dāng)x=-1時(shí)，2x²+4x-6有最小值，最小值是-8．
根據(jù)閱讀材料，利用“配方法”，解決下列問題：
（1）分解因式：a²-4a-5=
；
（2）已知△ABC的三邊長(zhǎng)a、b、c都是正整數(shù)，且滿足a²-4a+b²-12b+40=0求邊長(zhǎng)c的最小值；
（3）當(dāng)x、y為何值時(shí)，多項(xiàng)式-x²+2xy-2y²+6y+7有最大值？并求出這個(gè)最大值．
組卷：513引用：2難度：0.5
解析
26．在Rt△ABC中，∠BAC=90°，點(diǎn)D在邊BC上，AB=AD，點(diǎn)E在線段BD上，∠BAE=3∠EAD．
（1）如圖1，若點(diǎn)D與點(diǎn)C重合，則∠AEB=
°；
（2）如圖2，若點(diǎn)D與點(diǎn)C不重合，試說明∠C與∠EAD的數(shù)量關(guān)系；
（3）在（2）的情況下，試判斷BE，CD與AC的數(shù)量關(guān)系，并說明你的理由．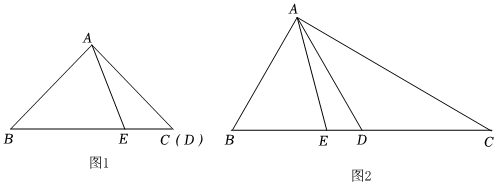
組卷：136引用：2難度：0.3
解析