2022-2023學年北京市大興區亦莊實驗中學高一（下）期末數學試卷

一、選擇題共10小題，每小題4分，共40分.在每小題列出的四個選項中，選出符合題目要求的一項.

• 1．已知復數z=-i（2+i），則z的共軛復數為（　　）

  A．1-2i

  B．2-i

  C．1+2i

  D．-1-2i
  組卷：157引用：4難度：0.8

  解析

• 2．設△ABC的內角A，B，C所對的邊分別為a,b,c,若a=

  3

  ，b=1，A=60°，則B等于（　　）

  A．30°

  B．45°

  C．60°

  D．150°
  組卷：357引用：3難度：0.7

  解析

• 3．若圓柱的軸截面是一個正方形，其面積為4S，則它的一個底面面積是 （　　）

  A．4S

  B．4πS

  C．πS

  D．2πS
  組卷：431引用：3難度：0.9

  解析

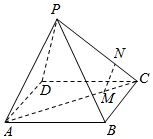• 4．如圖，四棱錐P-ABCD中，M，N分別為AC，PC上的點，且MN∥平面PAD，則（　　）

  A．MN∥PD	B．MN∥PA
  C．MN∥AD	D．以上均有可能
  組卷：6035引用：29難度：0.9

  解析

• 5．在下列四個正方體中，A、B為正方體的兩個頂點，M、N、Q為所在棱的中點，則在這四個正方體中，直線AB與平面MNQ不平行的是（　　）

  A．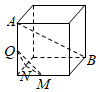

  B．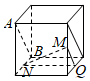

  C．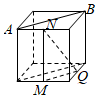

  D．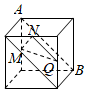
  組卷：945引用：40難度：0.6

  解析

• 6．閱讀下面題目及其證明過程，在橫線處應填寫的正確結論是（　　）
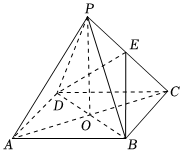
  如圖，四棱錐P-ABCD中，底面ABCD是正方形，O是正方形ABCD的中心，PO⊥底面ABCD，E是PC的中點，求證：平面PAC⊥平面BDE．
  證明：因為PO⊥底面ABCD，
  所以PO⊥BD．
  又因為AC⊥BD，且AC∩PO=O，
  所以__________．
  又因為BD?平面BDE，
  所以平面PAC⊥平面BDE．

  A．BD⊥平面PBC

  B．AC⊥平面PBD

  C．BD⊥平面PAC

  D．AC⊥平面BDE
  組卷：441引用：3難度：0.7

  解析

• 7．在△ABC中，若ac=8，a+c=7，

  B

  =

  π

  3

  ，則b=（　　）

  A．25

  B．5

  C．4

  D． 5
  組卷：1166引用：11難度：0.8

  解析

三、解答題共6小題，共85分.解答應寫出文字說明，演算步驟或證明過程.

• 20．在△ABC中，a+b=11，再從條件①、條件②這兩個條件中選擇一個作為已知，求：
  （Ⅰ）a的值；
  （Ⅱ）sinC和△ABC的面積．
  條件①：c=7，cosA=-

  1

  7

  ；
  條件②：cosA=

  1

  8

  ，cosB=

  9

  16

  ．
  注：如果選擇條件①和條件②分別解答，按第一個解答計分．
  組卷：5662引用：20難度：0.6

  解析

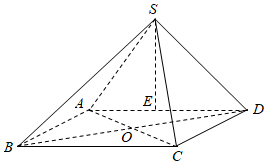• 21．如圖，在四棱錐S-ABCD中，底面ABCD是邊長為2的菱形，∠ABC=60°，SAD為正三角形．側面SAD⊥底面ABCD，E、F分別為棱AD、SB的中點．
  （Ⅰ）求證：AF∥平面SEC
  （Ⅱ）求證：平面ASB⊥平面CSB
  （Ⅲ）在棱SB上是否存在一點M，使得BD⊥平面MAC？若存在，求

  BM

  BS

  的值；若不存在，請說明理由．
  組卷：945引用：6難度：0.3

  解析