2022-2023學年遼寧省錦州市高二(下)期末數學試卷
發布:2024/6/27 8:0:9
一、選擇題:本題共8小題,每小題5分,共40分.在每小題給出的四個選項中,只有一項是符合題目要求的.
-
1.等差數列{an}中,a3=3,a7=27,則數列{an}的公差為( )
A.2 B.6 C.1 D.14 組卷:153引用:2難度:0.8 -
2.一箱產品中有6件正品和2件次品.每次從中隨機抽取1件進行檢測,抽出的產品不再放回.已知前兩次檢測的產品均是正品,則第三次檢測的產品是正品的概率為( )
A. 23B. 34C. 64125D. 715組卷:40引用:3難度:0.8 -
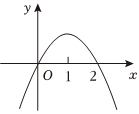 3.已知函數y=f(x)的導函數f′(x)的圖象如圖所示,則f(x)的圖象可能是( )
3.已知函數y=f(x)的導函數f′(x)的圖象如圖所示,則f(x)的圖象可能是( )A. 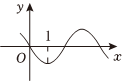
B. 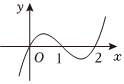
C. 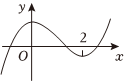
D. 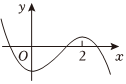 組卷:278引用:3難度:0.8
組卷:278引用:3難度:0.8 -
4.某商場為了了解毛衣的月銷售量y(件)與月平均氣溫x(℃)之間的關系,隨機統計了某4個月的月銷售量與當月平均氣溫,其數據如表:
由表中數據算出線性回歸方程月平均氣溫x(℃) 17 13 8 2 月銷售量y(件) 24 33 40 55 =bx+a中的b=-2,氣象部門預測下個月的平均氣溫約為8℃,據此估計該商場下個月毛衣銷售量約為( )件.?yA.40 B.42 C.46 D.48 組卷:48引用:3難度:0.7 -
5.康托(Cantor)是十九世紀末二十世紀初德國偉大的數學家,他創立的集合論奠定了現代數學的基礎.著名的“康托三分集”是數學理性思維的產物,具有典型的分形特征,其操作過程如下:將閉區間[0,1]均分為三段,去掉中間的區間段
,當記為第一次操作;再將剩下的兩個區間(13,23)分別均分為三段,并各自去掉中間的區間段,記為第二次操作:…,如此這樣,每次在上一次操作的基礎上,將剩下的各個區間分別均分為三段,同樣各自去掉中間的區間段.操作過程不斷地進行下去,以至無窮,剩下的區間集合即是“康托三分集”.若使“康托三分集”的各區間長度之和小于[0,13],[23,1],則需要操作的次數n的最小值為( )(參考數據:lg2=0.3010,lg3=0.4771)120A.6 B.8 C.10 D.12 組卷:32引用:2難度:0.5 -
6.已知
,設曲線y=lnx3-x3在x=k,k>0處的切線斜率為f(k),則( )a=2,b=log23,c=e2A.f(c)<f(b)<f(a) B.f(a)<f(c)<f(b) C.f(c)<f(a)<f(b) D.f(a)<f(b)<f(c) 組卷:169引用:2難度:0.6 -
7.班級舉行知識競猜闖關活動,設置了A,B,C三個問題.答題者可自行決定答三題順序.甲有60%的可能答對問題A,80%的可能答對問題B,50%的可能答對問題C.記答題者連續答對兩題的概率為p,要使得p最大,他應該先回答( )
A.問題A B.問題B C.問題A,B和C都可以 D.問題C 組卷:177引用:4難度:0.6
四、解答題:本題共6小題,共70分解答應寫出文字說明、證明過程或演算步驟.
-
21.2022北京冬奧會和冬殘奧會吉祥物冰墩墩、雪容融亮相上海展覽中心、為了慶祝吉祥物在上海的亮相,某商場舉辦了一場贏取吉祥物掛件的“定點投籃”活動,方案如下:
方案一:共投9次,每次投中得1分,否則得0分,累計所得分數記為Y;
方案二:共進行三輪投籃,每輪最多投三次,直到投中兩球為止得3分,否則得0分,三輪累計所得分數記為X.累計所得分數越多,所獲得獎品越多.現在甲準備參加這個“定點投籃”活動,已知甲每次投籃的命中率為P,每次投籃互不影響.
(1)若p=,甲選擇方案二,求第一輪投籃結束時,甲得3分的概率;12
(2)以最終累計得分的期望值為決策依據,甲在方案一,方案二之中選其一、應選擇哪個方案?組卷:103引用:4難度:0.6 -
22.已知函數f(x)=
.a2x2-x-xlnx(a∈R)
(1)若a=2,求方程f(x)=0的解;
(2)若f(x)有兩個零點且有兩個極值點,記兩個極值點為x1,x2,求a的取值范圍并證明f(x1)+f(x2)<.12e組卷:261引用:5難度:0.2


