2022-2023學年山東省青島市城陽實驗中學九年級（上）第一次月考數(shù)學試卷
發(fā)布：2024/4/20 14:35:0
一、選擇題（每題3分，共24分）
-
1．一元二次方程x2-2x=0的根是（ ）
組卷：5756引用：126難度：0.9 -
2．在下列命題中，正確的是（ ）
組卷：391引用：27難度：0.9 -
3．根據(jù)下列表格的對應(yīng)值：可得方程x2+5x-3=0一個解x的范圍是（ ）
x 0.00 0.25 0.50 0.75 1.00 x2+5x-3 -3.00 -1.69 -0.25 1.31 3.00 組卷：121引用：8難度：0.7 -
4．已知三角形兩邊長分別為2和9，第三邊的長為二次方程x2-14x+40=0的一個根，則這個三角形的周長為（ ）
組卷：56引用：5難度：0.7 -
5．順次連四邊形ABCD各邊中點得到四邊形EFGH，若四邊形EFGH的形狀是矩形，則原四邊形是（ ）
組卷：76引用：5難度：0.6 -
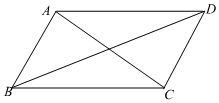6．如圖，四邊形ABCD是平行四邊形，從下列條件：①AB=BC，②∠ABC=90°，③AC=BD，④AC⊥BD中，選出其中兩個，使平行四邊形ABCD變?yōu)檎叫危旅娼M合錯誤的是（ ）組卷：626引用：5難度：0.6 -
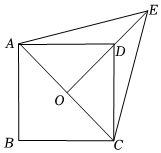7．如圖，O為正方形ABCD對角線AC的中點，△ACE為等邊三角形．若AB=2，則OE的長度為（ ）組卷：3085引用：20難度：0.6
四、解答題（共74分）
-
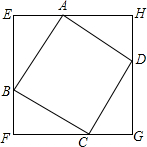22．如圖，正方形ABCD的四個頂點分別在正方形EFGH的四條邊上，我們稱正方形EFGH是正方形ABCD的外接正方形．
探究一：已知邊長為1的正方形ABCD，是否存在一個外接正方形EFGH，它的面積是正方形ABCD面積的2倍？如圖，假設(shè)存在正方形EFGH，它的面積是正方形ABCD的2倍．
因為正方形ABCD的面積為1，則正方形EFGH的面積為2，
所以EF=FG=GH=HE=，設(shè)EB=x,則BF=2-x,2
∵Rt△AEB≌Rt△BFC
∴BF=AE=-x2
在Rt△AEB中，由勾股定理，得
x2+（-x）2=122
解得，x1=x2=22
∴BE=BF，即點B是EF的中點．
同理，點C，D，A分別是FG，GH，HE的中點．
所以，存在一個外接正方形EFGH，它的面積是正方形ABCD面積的2倍
探究二：已知邊長為1的正方形ABCD，是否存在一個外接正方形EFGH，它的面積是正方形ABCD面積的3倍？（仿照上述方法，完成探究過程）
探究三：已知邊長為1的正方形ABCD，一個外接正方形EFGH，它的面積是正方形ABCD面積的4倍？（填“存在”或“不存在”）
探究四：已知邊長為1的正方形ABCD，是否存在一個外接正方形EFGH，它的面積是正方形ABCD面積的n倍？（n＞2）（仿照上述方法，完成探究過程）組卷：408引用：10難度：0.1 -
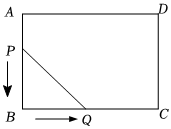23．如圖，在矩形ABCD中，AB=5cm,BC=6cm,點P從點A開始沿邊AB向終點B以1cm/s的速度移動，與此同時，點Q從點B開始沿邊BC向終點C以2cm/s的速度移動．如果P，Q分別從A，B同時出發(fā)，當點Q運動到點C時，兩點停止運動．設(shè)運動時間為t秒．（0＜t＜3）
（1）當t為何值時，點B在PQ的垂直平分線上？
（2）當t為何值時，PQ的長度等于5cm？
（3）連接PC，是否存在t的值，使得△PQC的面積等于8cm2？若存在，請求出此時t的值；若不存在，請說明理由．
（4）是否存在t的值，使得△BPQ的面積與五邊形APQCD的面積之比等于2：13？若存在，請求出此時t的值；若不存在，請說明理由．組卷：155引用：1難度：0.1