冀教版九年級（下）中考題單元試卷：第34章 二次函數（26）

一、選擇題（共1小題）

• 1．如圖，Rt△OAB的頂點A（-2，4）在拋物線y=ax²上，將Rt△OAB繞點O順時針旋轉90°，得到△OCD，邊CD與該拋物線交于點P，則點P的坐標為（　　）

  A．（ 2 ， 2 ）

  B．（2，2）

  C．（ 2 ，2）

  D．（2， 2 ）
  組卷：5917引用：94難度：0.4

  解析

二、解答題（共29小題）

• 2．如圖，已知拋物線y=-x²+6x-5．
  （1）若拋物線y=ax²+bx+c與y=-x²+6x-5關于原點O中心對稱，求此拋物線的解析式；
  （2）根據（1）的解題結果，合理猜想：直接寫出拋物線y=a（x-m）²+n關于原點O中心對稱的二次函數解析式（不要求寫推導過程）；
  （3）若（1）中拋物線y=ax²+bx+c與y軸交于點M，與x軸交于點A和點B（點A在左），點C是線段AB的中點，求sin∠CMA；
  （4）在（3）的條件下，在拋物線y=ax²+bx+c上是否存在點P，使△OPA的面積與△MCA的面積相等？若存在，求出點P的坐標；若不存在，請說明理由．
  組卷：224引用：51難度：0.5

  解析

• 3．如圖，拋物線m：y=-

  1

  4

  x²+

  3

  2

  x+4與x軸交于點A、B，頂點為M（3，

  25

  4

  ），將拋物線m繞點B旋轉180°得到新的拋物線n,此時A點旋轉至E點，M點旋轉至D點．
  （1）求A、B點的坐標；
  （2）求拋物線n的解析式；
  （3）若點P是線段ED上一個動點（E點除外），過點P作y軸的垂線，垂足為F，連接EF．如果P點的坐標為（x,y），△PEF的面積為s,求s與x的函數關系式，寫出自變量x的取值范圍；如果s有最大值，請求出s的最大值，如果沒有請說明理由；
  （4）設拋物線m的對稱軸與x軸的交點為G，以G為圓心，A、B兩點的距離為直
  徑作⊙G，試判斷直線CM與⊙G的位置關系，并說明理由．
  組卷：166引用：50難度：0.5

  解析

• 4．如圖，已知二次函數y=-（x+1）（x-m）的圖象與x軸相交于點A、B（點A在點B的左側），與y軸相交于點C，且圖象經過點M（2，3）．
  （1）求二次函數的解析式；
  （2）求ABC的面積；
  （3）在拋物線的對稱軸上找一點H，使AH+CH最小，并求出點H的坐標．
  組卷：260引用：52難度：0.5

  解析

• 5．如圖，拋物線y=ax²+bx+4的對稱軸是直線x=

  3

  2

  ，與x軸交于點A、B兩點，與y軸交于點C，并且點A的坐標為（-1，0）．
  （1）求拋物線的解析式；
  （2）過點C作CD∥x軸交拋物線于點D，連接AD交y軸于點E，連接AC，設△AEC的面積為S₁，△DEC的面積為S₂，求S₁：S₂的值．
  （3）點F坐標為（6，0），連接DF，在（2）的條件下，點P從點E出發，以每秒3個單位長的速度沿E→C→D→F勻速運動；點Q從點F出發，以每秒2個單位長的速度沿F→A勻速運動，當其中一點到達終點時，另外一點也隨之停止運動．若點P、Q同時出發，設運動時間為t秒，當t為何值時，以D、P、Q為頂點的三角形是直角三角形？請直接寫出所有符合條件的t值．
  組卷：21引用：50難度：0.5

  解析

• 6．如圖，在平面直角坐標系中，已知二次函數y=ax²+

  8

  3

  x+c的圖象與y軸交于點B（0，4），與x軸交于點A（-1，0）和點D．
  （1）求二次函數的解析式；
  （2）求△BOD內切圓的面積；
  （3）在拋物線上是否存在點P，使得△BOP的面積等于

  5

  2

  ？如果存在，那么這樣的點有幾個？如果不存在，請說明理由．
  組卷：265引用：50難度：0.5

  解析

• 7．如圖1．已知拋物線y=-

  1

  2

  x²+bx+c與x軸分別交于A，B兩點，與y軸交于點C，A點坐標為（-2，0），B的坐標為（4，0）．直線l過B，C兩點．點P是線段BC上的一個動點（點P不與B，C兩點重合）．在點P運動過程中，始終有一條過點P且和y軸平行的直線也隨之運動，該直線與拋物線的交點為M，與x軸的交點為N．
  （1）①求出拋物線的函數表達式；②直接寫出直線l的函數表達式；
  （2）若直線MN把△OBC的面積分成1：3的兩部分，求出此時點P的坐標．
  （3）如圖2，①連接BM，CM，設△MBC的面積是S，在點P的運動過程中，S是否存在最大值？若存在，請求出這個最大值；若不存在，請說明理由．
  ②當△MBC的面積最大時，直線MN上另有一動點E，在坐標平面內是否存在點F，使以點A，P，E，F為頂點的四邊形為菱形？若存在，請直接寫出點F的坐標；若不存在，請說明理由．
  
  組卷：623引用：50難度：0.5

  解析

• 8．如圖1，已知在平面直角坐標系中，拋物線y=ax²+bx+3經過A（-1，0），B（3，0）兩點，且與y軸交于點C．
  （1）求拋物線的解析式及頂點D的坐標；
  （2）設△COB沿x軸正方向平移t（0＜t≤3）個單位長度時，△COB與△CDB重疊部分的面積為S，求S與t之間的函數關系式，并指出t的取值范圍；
  考生請注意：下面的（3），（4），（5）題為三選一的選做題，即只能選做其中一個題目，多答時只按作答的首題評分，切記喲！
  （3）點P是x軸上的一個動點，過點P作直線l∥AC交拋物線于點Q，試探究：隨著P點的運動，在拋物線上是否存在點Q，使以點A、P、Q、C為頂點的四邊形是平行四邊形？若存在，請直接寫出符合條件的點Q的坐標；若不存在，請說明理由；
  （4）設點Q是y軸右側拋物線上異于點B的點，過點Q作QP∥x軸交拋物線于另一點P，過P作PH⊥x軸，垂足為H，過Q作QG⊥x軸，垂足為G，則四邊形QPHG為矩形．試探究在點Q運動的過程中矩形QPHG能否成為正方形？若能，請直接寫出符合條件的點Q的坐標；若不能，請說明理由；
  （5）試探究，在y軸右側的拋物線上是否存在一點Q，使△QDC是等腰三角形？若存在，請直接寫出符合條件的點Q坐標；若不存在，請說明理由．
  
  組卷：405引用：50難度：0.5

  解析

• 9．已知二次函數y=x²-2mx+m²-1．
  （1）當二次函數的圖象經過坐標原點O（0，0）時，求二次函數的解析式；
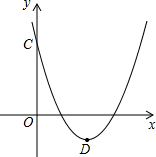
  （2）如圖，當m=2時，該拋物線與y軸交于點C，頂點為D，求C、D兩點的坐標；
  （3）在（2）的條件下，x軸上是否存在一點P，使得PC+PD最短？若P點存在，求出P點的坐標；若P點不存在，請說明理由．
  組卷：2927引用：87難度：0.5

  解析

• 10．如圖，直線x=-4與x軸交于點E，一開口向上的拋物線過原點交線段OE于點A，交直線x=-4于點B，過B且平行于x軸的直線與拋物線交于點C，直線OC交直線AB于D，且AD：BD=1：3．
  （1）求點A的坐標；
  （2）若△OBC是等腰三角形，求此拋物線的函數關系式．
  組卷：1292引用：53難度：0.5

  解析

二、解答題（共29小題）

• 29．如圖1，在平面直角坐標系中，二次函數y=-

  4

  27

  x²+12的圖象與y軸交于點A，與x軸交于B，C兩點（點B在點C的左側），連接AB，AC．
  
  （1）點B的坐標為

  ，點C的坐標為

  ；
  （2）過點C作射線CD∥AB，點M是線段AB上的動點，點P是線段AC上的動點，且始終滿足BM=AP（點M不與點A，點B重合），過點M作MN∥BC分別交AC于點Q，交射線CD于點N （點Q不與點P重合），連接PM，PN，設線段AP的長為n.
  ①如圖2，當n＜

  1

  2

  AC時，求證：△PAM≌△NCP；
  ②直接用含n的代數式表示線段PQ的長；
  ③若PM的長為

  97

  ，當二次函數y=-

  4

  27

  x²+12的圖象經過平移同時過點P和點N時，請直接寫出此時的二次函數表達式．
  組卷：3099引用：50難度：0.1

  解析

• 30．已知拋物線經過A（-2，0），B（0，2），C（

  3

  2

  ，0）三點，一動點P從原點出發以1個單位/秒的速度沿x軸正方向運動，連接BP，過點A作直線BP的垂線交y軸于點Q．設點P的運動時間為t秒．
  （1）求拋物線的解析式；
  （2）當BQ=

  1

  2

  AP時，求t的值；
  （3）隨著點P的運動，拋物線上是否存在一點M，使△MPQ為等邊三角形？若存在，請直接寫t的值及相應點M的坐標；若不存在，請說明理由．
  
  組卷：4204引用：52難度：0.1

  解析