當前位置：試卷中心 > 試卷詳情

2022-2023學年廣東省江門市普通高中高三（上）調研數學試卷

發布：2024/4/20 14:35:0

一、選擇題：本題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的.

1．已知集合A={x|1≤x≤4}，B={x∈N₊|x²-2x≤3}，則A∩B=（　　）
A．{x|1≤x≤3} B．{x|0≤x≤3} C．{1，2，3} D．{0，1，2，3}
組卷：30引用：1難度：0.7
解析
2．已知p：x+y≠4，q：x,y不都是2，則p是q的（　　）
A．充分不必要條件 B．必要不充分條件
C．充要條件 D．既不充分也不必要條件
組卷：39引用：1難度：0.7
解析
3．已知
a
=
c
+
3
+
c
+
4
，
b
=
c
+
2
+
c
+
5
，則（　　）
A．a＞b＞1 B．b＞a＞1 C．a＞1＞b D．b＞1＞a
組卷：95引用：2難度：0.7
解析
4．已知函數f（x）=x²（e^x-e^-x）+2，若f（t）=4，則f（-t）的值為（　　）
A．-1 B．0 C．1 D．2
組卷：95引用：1難度：0.7
解析
5．在
（
x
2
+
x
+
1
）
（
1
x
-
1
）
5
的展開式中常數項為（　　）
A．14 B．-14 C．6 D．-6
組卷：507引用：4難度：0.7
解析
6．在△ABC中，內角A，B，C的對邊長分別為a,b,c,且tanA+3tan（A+B）=0，a²-c²=2b,則b的值為（　　）
A．6 B．5 C．4 D．3
組卷：213引用：1難度：0.5
解析
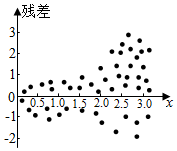7．根據變量Y和x的成對樣本數據，由一元線性回歸模型
Y
=
bx
+
a
+
e
,
E
（
e
）
=
0
，
D
（
e
）
=
σ
2
得到線性回歸模型
?
y
=
?
b
x
+
?
a
，對應的殘差如圖所示，模型誤差（　　）
A．滿足一元線性回歸模型的所有假設
B．滿足回歸模型E（e）=0的假設
C．滿足回歸模型D（e）=σ²的假設
D．不滿足回歸模型E（e）=0和D（e）=σ²的假設
組卷：133引用：3難度：0.8
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、解答題：共70分.解答應寫出文字說明、證明過程或演算步驟.

21．通過驗血能篩查乙肝病毒攜帶者，統計專家提出一種β化驗方法：隨機地按k人一組進行分組，然后將每組k個人的血樣混合化驗．如果混合血樣呈陰性，說明這k人全部陰性；如果混合血樣呈陽性，說明這k人中至少有一人血樣呈陽性，需要重新采集這k人血樣并分別化驗一次，從而確定乙肝病毒攜帶者．
（1）已知某單位有1000名職工，假設其中有2人是乙肝病毒攜帶者，如果將這1000人隨機分成100組，每組10人，且每組都采用β化驗方法進行化驗．
（i）若兩名乙肝病毒攜帶者被分到同一組，求本次化驗的總次數；
（ii）假設每位職工被分配到各組的機會均等，設X是化驗的總次數，求X的分布列與數學期望E（X）．
（2）現采用β化驗方法，通過驗血大規模篩查乙肝病毒攜帶者．為方便管理、采樣、化驗，每組人數宜在10至12人之間．假設每位被篩查對象的乙肝病毒攜帶率均為2%，且相互獨立，每組k（k∈N₊，10≤k≤12）人．設每人平均化驗次數為Y，以Y的數學期望E（Y）為依據，確定使化驗次數最少的k的值．
參考數據：0.98¹⁰≈0.82，0.98¹¹≈0.80，0.98¹²≈0.78，數據保留兩位小數．
組卷：87引用：1難度：0.6
解析
22．已知函數
f
（
x
）
=
（
a
+
1
a
）
lnx
+
1
x
-x（a＞0），函數g（x）是定義在（0，+∞）的可導函數，其導數為g'（x），滿足0＜g（x）＜-g'（x）．
（1）令函數G（x）=e^xg（x），求證：G（x）在（0，+∞）上是減函數；
（2）若f（x）在（0，+∞）上單調遞減，求實數a取值范圍；
（3）對任意正數x₁，x₂（x₁＜x₂），試比較
x
2
1
g
（
x
1
x
2
）
與
x
2
2
g
（
x
2
x
1
）
的大小．
組卷：21引用：1難度：0.6
解析