2022-2023學(xué)年江西省宜春市宜豐中學(xué)高三（上）期末數(shù)學(xué)試卷

一、單選題（共40分）

• 1．已知集合A={x|1＜x＜3}，集合B={x|log₂（x+1）≤2}，則A∪B=（　　）

  A．{x|1＜x＜3}

  B．{x|x≤3}

  C．{x|-1＜x＜3}

  D．{x|-1＜x≤3}
  組卷：67引用：4難度：0.8

  解析

• 2．已知等差數(shù)列{a_n}滿足

  a

  8

  a

  5

  =

  -

  2

  ，則下列結(jié)論一定成立的是（　　）

  A． a 9 a 4 = - 1

  B． a 8 a 3 = - 1

  C． a 9 a 3 = - 1

  D． a 10 a 4 = - 1
  組卷：133引用：2難度：0.7

  解析

• 3．命題“?x∈R，mx²-2mx+1＞0”是假命題，則實(shí)數(shù)m的取值范圍為（　　）

  A．0≤m＜1

  B．m＜0或m≥1

  C．m≤0或m≥1

  D．0＜m＜1
  組卷：382引用：4難度：0.8

  解析

• 4．函數(shù)

  f

  （

  x

  ）

  =

  5

  sinx

  e

  |

  x

  |

  +

  xcosx

  在[-2π，2π]上的圖象大致為（　　）

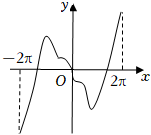
  A．	B．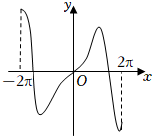
  C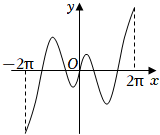．	D．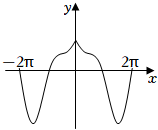
  組卷：689引用：22難度：0.7

  解析

• 5．已知函數(shù)f（x）=a^x-ax（a＞1），且f（x）在[1，2]有兩個(gè)零點(diǎn)，則a的取值范圍為（　　）

  A．（1，2]

  B．（1，e）

  C．[2，e）

  D．（e,e2]
  組卷：49引用：3難度：0.5

  解析

• 6．已知10^0.4771≈3，10^0.301≈2，設(shè)M=15¹⁰，則M所在的區(qū)間為（　　）

  A．（109，1010）	B．（1010，1011）
  C．（1011，1012）	D．（1012，1013）
  組卷：57引用：1難度：0.6

  解析

• 7．若

  α

  ，

  β

  ∈

  （

  π

  2

  ，

  π

  ）

  ，且（1-cos2α）（1+sinβ）=sin2αcosβ，則下列結(jié)論正確的是（　　）

  A． 2 α + β = 5 π 2

  B． 2 α - β = 3 π 4

  C． α + β = 7 π 4

  D． α - β = π 2
  組卷：667引用：7難度：0.6

  解析

四、解答題（共70分）

• 21．已知函數(shù)f（x）=2x³-ax²+b.
  （1）討論f（x）的單調(diào)性；
  （2）是否存在a,b,使得f（x）在區(qū)間[0，1]的最小值為-1且最大值為1？若存在，求出a,b的所有值；若不存在，說明理由．
  組卷：8377引用：22難度：0.1

  解析

• 22．已知橢圓C：

  x

  2

  4

  +

  y

  2

  3

  =1的左、右頂點(diǎn)分別為A，B，右焦點(diǎn)為F，折線|x-1|=my（m≠0）與C交于M，N兩點(diǎn)．
  （1）當(dāng)m=2時(shí)，求|MF|+|NF|的值；
  （2）直線AM與BN交于點(diǎn)P，證明：點(diǎn)P在定直線上．
  組卷：786引用：7難度：0.6

  解析