2022年天津市靜海一中高考數學調研試卷（5月份）

一、選擇題.

• 1．已知集合

  A

  =

  {

  6

  x

  +

  1

  ∈

  N

  |

  x

  ∈

  N

  }

  ，B={x|x²-7x+10≤0}，則A∩B=（　　）

  A．{x|2≤x＜5}

  B．{x|2≤x≤5}

  C．{2，5}

  D．{2，3}
  組卷：181引用：2難度：0.7

  解析

• 2．設x∈R，則“x＜1”是“x|x|-2＜0”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充要條件	D．既不充分也不必要條件
  組卷：452引用：13難度：0.7

  解析

• 3．設a=ln3，b=

  log

  1

  e

  3，c=3^-2，則（　　）

  A．a＞b＞c

  B．b＞a＞c

  C．a＞c＞b

  D．c＞b＞a
  組卷：707引用：9難度：0.7

  解析

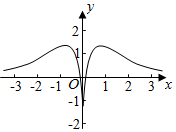• 4．已知函數f（x）的部分圖象如圖所示，則f（x）的解析式可能為（　　）

  A． f （ x ） = 4 + ln | x | 1 + 1 2 cosx	B． f （ x ） = x 2 cosx e | x |
  C． f （ x ） = cosx ? ln | x | 2 + sinx	D． f （ x ） = 2 + ln | x | x 2 + cosx
  組卷：216引用：3難度：0.6

  解析

• 5．已知10^x=2，10^y=5，則（　　）

  A．x+y＜1

  B． xy ＞ 1 4

  C． x 2 + y 2 ＞ 1 2

  D． y - x ＞ 2 5
  組卷：354引用：4難度：0.8

  解析

• 6．已知雙曲線

  y

  2

  a

  2

  -

  x

  2

  b

  2

  =

  1

  （

  a

  ＞

  0

  ，

  b

  ＞

  0

  ）

  的一條漸近線過點

  （

  3

  ，

  2

  ）

  ，且雙曲線的一個焦點在拋物線

  x

  2

  =

  4

  7

  y

  的準線上，則雙曲線的方程為（　　）

  A． y 2 21 - x 2 28 = 1	B． x 2 28 - y 2 21 = 1
  C． x 2 4 - y 2 3 = 1	D． y 2 4 - x 2 3 = 1
  組卷：745引用：7難度：0.7

  解析

三、解答題：解答應寫出必要的文字說明、推證過程或演算步驟．

• 19．已知數列{a_n}滿足：a₁=3，a_n=a_n-1+2^n-1（n≥2，n∈N^*）．
  （1）求數列{a_n}的通項；
  （2）若b_n=n（a_n-1）（n∈N^*），求數列{b_n}的前n項和S_n；
  （3）設c_n=

  1

  a

  n

  a

  n

  +

  1

  ，T_n=2c₁+2²c₂+…+2ⁿc_n（n∈N^*），求證：

  2

  15

  ≤

  T

  n

  ＜

  1

  3

  （

  n

  ∈

  N

  *

  ）

  ．
  組卷：654引用：5難度：0.7

  解析

• 20．已知函數

  f

  （

  x

  ）

  =

  x

  ?

  ln

  a

  x

  （

  a

  ＞

  0

  ）

  ．
  （1）若函數g（x）=e^x在x=0處的切線也是函數f（x）圖象的一條切線，求實數a的值；
  （2）若函數f（x）的圖象恒在直線x-y+1=0的下方，求實數a的取值范圍；
  （3）若

  x

  1

  ，

  x

  2

  ∈

  （

  a

  e

  ，

  a

  2

  ）

  ，且x₁≠x₂，證明：

  （

  x

  1

  +

  x

  2

  ）

  4

  ＞a²x₁x₂．
  組卷：224引用：2難度：0.3

  解析