當前位置：試卷中心 > 試卷詳情

2021-2022學年江蘇省鹽城市鹽都區鹿鳴路初中教育集團八年級（下）期中數學試卷

發布：2024/4/20 14:35:0

一、精心選一選：（本大題共有8小題，每小題2分，共16分）

1．下列四個圖案中是中心對稱圖形的是（　　）
A． B． C． D．
組卷：14引用：3難度：0.9
解析
2．下列二次根式中，最簡二次根式的是（　　）
A．
8
B．
6
C．
1
3
D．
1
2
組卷：383引用：4難度：0.8
解析
3．若
3
x
-
1
在實數范圍內有意義，則x的取值范圍是（　　）
A．x≥
1
3
B．x≤
1
3
C．x＞
1
3
D．x≠
1
3
組卷：813引用：7難度：0.8
解析
4．下列各點在反比例函數
y
=
6
x
圖象上的是（　　）
A．（2，-3） B．（-2，3） C．（3，2） D．（3，-2）
組卷：130引用：4難度：0.9
解析
5．下列條件中，能判定四邊形是平行四邊形的是（　　）
A．一組對邊平行 B．對角線互相平分
C．一組對邊相等 D．對角線互相垂直
組卷：670引用：9難度：0.7
解析
6．下列二次根式中，與
12
是同類二次根式的是（　　）
A．
2
B．
6
C．
5
D．
3
組卷：37引用：4難度：0.8
解析
7．小甘為測量池塘邊A，B兩點的距離，在線段AB側選取一點P，連接PA并延長至
點M，連接PB并延長至點N，使得AM=PA，BN=PB，如圖．若測得MN=8米，則點
A，B的距離為（　　）
A．16米 B．6米 C．4米 D．2米
組卷：454引用：6難度：0.5
解析
8．若反比例函數
y
=
-
1
+
a
2
x
的圖象上有兩點A（-1，m），B（2，n），則m,n的關系是（　　）
A．m＞n B．m＜n C．m≥n D．m≤n
組卷：40引用：3難度：0.6
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

三、認真答一答：（本大題共8小題，共64分）

25．【概念理解】若一條直線l把一個圖形分成面積相等的兩個圖形，則稱這樣的直線l叫做這個圖形的等積直線．如圖1，直線l經過三角形ABC的頂點A和邊BC的中點N，易知直線l將△ABC分成兩個面積相等的圖形，則稱直線l為△ABC的等積直線．

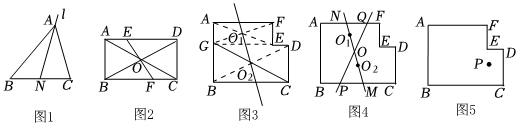
（1）如圖2，矩形ABCD對角線AC，BD相交于點O，直線EF過點O，分別交AD，BC于點E，F．
①求證：AE=CF．
②請你判斷直線EF是否為該矩形的等積直線．
．（填“是”或“不是”）
（2）【問題探究】如圖3是一個缺角矩形，其中∠A=∠B=∠C=∠D=∠E=∠F=90°，小華同學給出了該圖形等積直線的一個作圖方案：將這個圖形分成矩形AGEF、矩形GBCD，這兩個矩形的對稱中心O₁，O₂所在直線是該缺角矩形的等積直線．
如圖4，直線O₁O₂是該圖形的一條等積直線，它與邊BC，AF分別交于點M，N，過MN的中點O的直線分別交邊BC，AF于點P，Q，直線PQ
（填“是”或“不是”）缺角矩形ABCDEF的等積直線．
（3）【實際應用】若缺角矩形ABCDEF是老張家的一塊田地如圖5．P為水井，現要把這塊田地平均分給兩個兒子，為了灌溉方便，便想使每個兒子分得的土地都有一邊和水井相鄰，試問該如何分割這塊土地？畫出圖形，并說明理由．
組卷：149引用：5難度：0.2
解析
26．某數學興趣小組利用正方形硬紙片開展了一次活動，請閱讀下面的探究片段，完成所提出的問題．
四邊形ABCD是邊長為3正方形，點E是射線BC上的動點，∠AEF=90°，且EF交正方形外角的平分線CF于點F．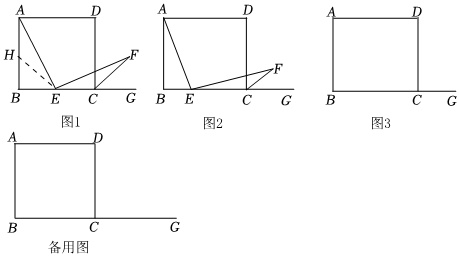

【探究1】當點E是BC中點時如圖1，發現AE=EF，這需要證明AE與EF所在的兩個三角形全等，但△ABE與△FCE顯然不全等，考慮到點E是BC的中點，取AB的中點H，連接EH，證明△AHE與△ECF全等即可．
【探究2】
（1）如圖2，如果把“點E是邊BC的中點”改為“點E是邊BC上（不與點B、C重合）的任意一點”，其他條件不變，那么結論“AE=EF”仍然成立嗎？如果成立，寫出證明過程，如果不成立，請說明理由；
（2）如圖3，如果點E是邊BC延長線上的任意一點，其他條件不變，請你畫出圖形，并判斷“AE=EF”是否成立？
（填“是”或“否”）；
【探究3】
（3）連接AF交直線CD于點I，連接EI，試探究線段BE，EI，ID之間的數量關系，并說明理由．
組卷：185引用：3難度：0.1
解析