2021-2022學年浙江省金華市十校高一（下）期末數學試卷

一、選擇題：本題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的.

• 1．已知集合A={x|x=3n+1，n∈N}，集合B={3，4，5，6，7，8，10}，則A∩B中元素的個數為（　　）

  A．1

  B．2

  C．3

  D．4
  組卷：211引用：1難度：0.9

  解析

• 2．已知向量

  a

  =（1，2），

  b

  =（3，4），則

  a

  -

  b

  =（　　）

  A．（2，6）

  B．（-2，6）

  C．（4，6）

  D．（-2，-2）
  組卷：232引用：3難度：0.9

  解析

• 3．幾何學中把變換前后兩點間距離保持不變的變換稱為剛體變換，在平面中作圖形變換，易知平移變換是一種剛體變換，以下兩個函數f（x）與g（x），其中g（x）可以由f（x）通過平移得到的是（　　）

  A． f （ x ） = sin 4 x , g （ x ） = cos （ π 6 - 4 x ）

  B．f（x）=x2，g（x）=3x2+4

  C． f （ x ） = 3 x + 3 - 2 ， g （ x ） = 2 3 - x + 3

  D．f（x）=4x+1，g（x）=5x
  組卷：77引用：1難度：0.8

  解析

• 4．高斯是德國著名的數學家，近代數學奠基者之一，享有“數學王子”的美譽，用其名字命名的“高斯函數“：設x∈R，用[x]表示不超過x的最大整數，則y=[x]稱為高斯函數，也稱取整函數，例如：[-1.3]=-2，[3.4]=3，已知

  f

  （

  x

  ）

  =

  1

  3

  x

  +

  1

  -

  1

  3

  ，則函數y=[f（x）]的值域為（　　）

  A．{0}

  B．{-1，0}

  C．{0，1}

  D．{-1，0，1}
  組卷：484引用：1難度：0.5

  解析

• 5．已知α∈R，則函數

  f

  （

  x

  ）

  =

  x

  α

  x

  2

  +

  1

  的圖像不可能是（　　）

  A．

  B．

  C．

  D．
  組卷：113引用：3難度：0.7

  解析

• 6．如圖，小呂考慮用一個棱長為12mm的正四面體硬木件V-ABC，削磨出一個體積最大的球，他的第一步是削去一個小正四面體V-A₁B₁C₁，則截面△A₁B₁C₁面積的最大值為（　　）

  A． 2 3 mm 2

  B． 9 3 4 mm 2

  C． 4 3 mm 2

  D． 9 3 mm 2
  組卷：203引用：1難度：0.6

  解析

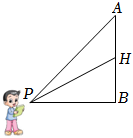• 7．如圖所示，唐唐在背景墻上安裝了一臺視頻監視器，P為唐唐坐在工位上時相當于眼睛位置的一點，P在背景墻上的水平投影點為B，過B作垂直于地面的直線AB，分別交監視器上、下端于A、H兩點，測得AB=2m,BH=1.5m,若∠APB=α，∠HPB=β，則α-β為唐唐看監視器的視角．唐唐通過調整工位使視角取得最大值，此時PB的長為（　　）

  A． 3 m

  B． 6 m

  C．2m

  D． 4 2 3 m
  組卷：178引用：2難度：0.6

  解析

四、解答題：本題共6小題，共70分.解答應寫出文字說明、證明過程或演算步驟.

• 21．如圖，在三棱柱：ABC-A₁B₁C₁中，AB⊥AC，AB=AC=2，點D為線段BC中點，側面BCC₁B₁為矩形．
  （Ⅰ）證明：平面A₁AD⊥平面BCC₁B₁；
  （Ⅱ）若

  ∠

  A

  1

  AB

  =

  2

  π

  3

  ，二面角A-BC-A₁的正切值為

  1

  2

  ，求CC₁與平面A₁BC所成角的正弦值．
  組卷：395引用：1難度：0.5

  解析

• 22．已知函數

  f

  （

  x

  ）

  =

  x

  2

  -

  2

  a

  x

  -

  1

  ，

  a

  ＞

  0

  ．
  （Ⅰ）當a=1時，求f（x）在區間[4，8]上的值域；
  （Ⅱ）函數g（x）=x|x-a|，若對任意x₀∈[4，8]，存在x₁，x₂∈[4，8]，且x₁≠x₂，使得g（x₁）=g（x₂）=f（x₀），求a的范圍．
  組卷：504引用：1難度：0.2

  解析