人教新版九年級上冊《22.3 二次函數與實際問題》2021年同步練習卷（1）

一、選擇題

• 1．一件工藝品進價為100元，標價135元售出，每天可售出100件．根據銷售統計，一件工藝品每降價1元出售，則每天可多售出4件，要使每天獲得的利潤最大，每件需降價的錢數為（　　）

  A．5元

  B．10元

  C．0元

  D．36元
  組卷：1203引用：33難度：0.7

  解析

• 2．某產品進貨單價為9元，按10元一件出售時，能售出50件．若每件每漲價1元，銷售量就減少10件，則該產品能獲得的最大利潤為（　　）

  A．50元

  B．80元

  C．90元

  D．100元
  組卷：82引用：2難度：0.6

  解析

• 3．據省統計局公布的數據，安徽省2019年第二季度GDP總值約為7.9千億元人民幣，若我省第四季度GDP總值為y千億元人民幣，平均每個季度GDP增長的百分率為x,則y關于x的函數表達式是（　　）

  A．y=7.9（1+2x）

  B．y=7.9（1-x）2

  C．y=7.9（1+x）2

  D．y=7.9+7.9（1+x）+7.9（1+x）2
  組卷：1355引用：9難度：0.8

  解析

• 4．某商店從廠家每件21元的價格購進一批商品，該商店可以自行定價．若每件商品售為x元，則可賣出（350-10x）件商品，那商品所賺錢y元與售價x元的函數關系為（　　）

  A．y=-10x2-560x+7350	B．y=-10x2+560x-7350
  C．y=-10x2+350x	D．y=-10x2+350x-7350
  組卷：925引用：7難度：0.9

  解析

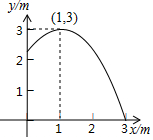• 5．如圖，池中心豎直水管的頂端安一個噴水頭，使噴出的拋物線形水柱在與池中心的水平距離為1m處達到最高，高度為3m,水柱落地處離池中心3m,水管的長為（　　）

  A．2.1m

  B．2.2m

  C．2.3m

  D．2.25m
  組卷：822引用：9難度：0.7

  解析

三、解答題

• 15．某商品的進價為每件20元，售價為每件30元，每月可賣出180件．如果該商品的售價每上漲1元，就會少賣出10件，但每件售價不能高于35元，設每件商品的售價上漲x元（x為整數）時，月銷售利潤為y元．
  （1）求y與x之間的函數解析式，并直接寫出自變量x的取值范圍．
  （2）當每件商品的售價定為多少元時，可獲得的月利潤最大？最大月利潤是多少？
  組卷：1193引用：11難度：0.8

  解析

• 16．已知某商品的進價為每件40元．現在的售價是每件60元．每星期可賣出300件．市場調查反映：如調整價格，每漲價一元．每星期要少賣出10件；每降價一元，每星期可多賣出18件．如何定價才能使利潤最大？
  組卷：173引用：4難度：0.6

  解析