2013-2014學年湖北省黃岡市啟黃中學九年級（下）入學數學試卷

一、選擇題（每小題3分，共24分）

• 1．-2的倒數是（　　）

  A．-2

  B．- 1 2

  C． 1 2

  D．2
  組卷：4003引用：688難度：0.9

  解析

• 2．如圖所示，該幾何體的主視圖應為（　　）
  

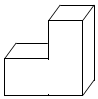
  A．

  B．

  C．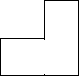

  D．
  組卷：9引用：13難度：0.9

  解析

• 3．下列計算正確的是（　　）

  A．a3-a=a2

  B．（-2a）2=4a2

  C．x3?x-2=x-6

  D．x6÷x2=x3
  組卷：57引用：6難度：0.9

  解析

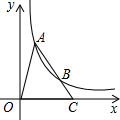• 4．如圖，A、B是雙曲線

  y

  =

  k

  x

  （

  k

  ＞

  0

  ）

  上的點，A、B兩點的橫坐標分別是a、3a,線段AB的延長線交x軸于點C，若S_△AOC=6，則k的值為（　　）

  A．2

  B．3

  C．4

  D．6
  組卷：1456引用：4難度：0.9

  解析

• 5．如果將一組數據中的每一個數據都加上同一個非零常數，那么這組數據的（　　）

  A．平均數和方差都不變	B．平均數不變，方差改變
  C．平均數改變，方差不變	D．平均數和方差都改變
  組卷：88引用：23難度：0.9

  解析

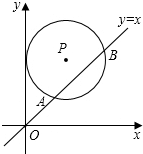• 6．如圖，在平面直角坐標系中，⊙P的圓心是（2，a）（a＞2），半徑為2，函數y=x的圖象被⊙P截得的弦AB的長為

  2

  3

  ，則a的值是（　　）

  A．2 2

  B．2+ 2

  C．2 3

  D．2+ 3
  組卷：3873引用：75難度：0.4

  解析

• 7．已知：M，N兩點關于y軸對稱，且點M在雙曲線

  y

  =

  1

  2

  x

  上，點N在直線y=x+3上，設點M的坐標為（a,b），則二次函數y=-abx²+（a+b）x（　　）

  A．有最大值，最大值為 - 9 2	B．有最大值，最大值為 9 2
  C．有最小值，最小值為 9 2	D．有最小值，最小值為 - 9 2
  組卷：815引用：11難度：0.9

  解析

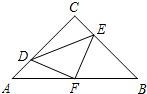• 8．如圖，在等腰Rt△ABC中，∠C=90°，AC=8，F是AB邊上的中點，點D，E分別在AC，BC邊上運動，且保持AD=CE．連接DE，DF，EF．在此運動變化的過程中，下列結論：
  ①△DFE是等腰直角三角形；
  ②四邊形CDFE不可能為正方形，
  ③DE長度的最小值為4；
  ④四邊形CDFE的面積保持不變；
  ⑤△CDE面積的最大值為8．
  其中正確的結論是（　　）

  A．①②③

  B．①④⑤

  C．①③④

  D．③④⑤
  組卷：1810引用：68難度：0.7

  解析

三、解答題（共計75分）

• 23．某公司開發了一種新型的家電產品，又適逢“家電下鄉”的優惠政策．現投資40萬元用于該產品的廣告促銷，已知該產品的本地銷售量y₁（萬臺）與本地的廣告費用x（萬元）之間的函數關系滿足y₁=

  3 x （ 0 ≤ x ≤ 25 ）

  2 x + 25 （ 25 ≤ x ≤ 40 ）

  ．該產品的外地銷售量y₂（萬臺）與外地廣告費用t（萬元）之間的函數關系可用如圖所示的拋物線和線段AB來表示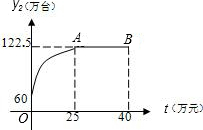．其中點A為拋物線的頂點．
  （1）結合圖象，求出y₂（萬臺）與外地廣告費用t（萬元）之間的函數關系式；
  （2）求該產品的銷售總量y（萬臺）與本地廣告費用x（萬元）之間的函數關系式；
  （3）如何安排廣告費用才能使銷售總量最大？
  組卷：281引用：6難度：0.3

  解析

• 24．已知，如圖，在平面直角坐標系中，點A坐標為（-2，0），點B坐標為（0，2），點E為線段AB上的動點（點E不與點A，B重合），以E為頂點作∠OET=45°，射線ET交線段OB于點F，C為y軸正半軸上一點，且OC=AB，拋物線y=-

  2

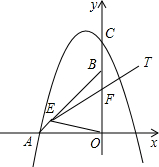  x²+mx+n的圖象經過A，C兩點．
  （1）求此拋物線的函數表達式；
  （2）求證：∠BEF=∠AOE；
  （3）當△EOF為等腰三角形時，求此時點E的坐標；
  （4）在（3）的條件下，當直線EF交x軸于點D，P為（1）中拋物線上一動點，直線PE交x軸于點G，在直線EF上方的拋物線上是否存在一點P，使得△EPF的面積是△EDG面積的（2

  2

  +1）倍？若存在，請直接寫出點P的坐標；若不存在，請說明理由．
  組卷：1228引用：10難度：0.5

  解析