當前位置：試卷中心 > 試卷詳情

2022-2023學年廣東省深圳實驗學校初中部八年級（下）期中數學試卷

發布：2024/4/29 8:6:34

一、選擇題（每小題3分，共30分）

1．下列圖形是中心對稱圖形的是（　　）
A． B． C． D．
組卷：820引用：6難度：0.9
解析
2．分式
3
2
-
x
中x的取值范圍是（　　）
A．x≠2 B．x≠-2 C．x≤-2 D．x≤2
組卷：741引用：6難度：0.9
解析
3．下面各式從左到右的變形，屬于因式分解的是（　　）
A．x²-x-1=x（x-1）-1 B．x²-1=（x-1）²
C．x²-x-6=（x-3）（x+2） D．x（x-1）=x²-x
組卷：3227引用：30難度：0.5
解析
4．若等腰三角形的兩邊長分別是3cm和5cm,則這個等腰三角形的周長是（　　）
A．8cm B．13cm C．8cm或13cm D．11cm或13cm
組卷：2602引用：22難度：0.5
解析
5．下列命題是真命題的是（　　）
A．一個角的補角一定大于這個角
B．平行于同一條直線的兩條直線平行
C．等邊三角形是中心對稱圖形
D．旋轉改變圖形的形狀和大小
組卷：684引用：8難度：0.6
解析
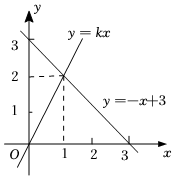6．根據圖象，可得關于x的不等式kx＞-x+3的解集是（　　）
A．x＜2 B．x＞2 C．x＜1 D．x＞1
組卷：3377引用：14難度：0.6
解析
7．如圖，在△ABC中，∠C=90°，AC=8，DC=
1
3
AD，BD平分∠ABC，則點D到AB的距離等于（　　）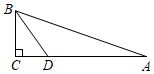
A．4 B．3 C．2 D．1
組卷：4166引用：39難度：0.6
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

三、解答題（16題8分，17題6分，18題7分，19題7分，20題8分，21題9分，22題10分）

21．如圖，在平面直角坐標系中，O為原點，點A（6，0），點B在y軸的正半軸上，∠ABO=30°，矩形CODE的頂點D，E，C分別在OA，AB，OB上，OD=2，將矩形CODE平移，平移后的矩形為C′O′D′E′．
（1）如圖1，將矩形CODE沿著x軸的正方向以每秒1個單位長度的速度平移，設平移的時間為t秒．
①若t=2時，線段D′E′與線段AB相交于點F，求此時△AD′F的面積；
②若直線AB平分矩形C′O′D′E′的面積，求此時t的值；
（2）如圖2，將矩形CODE沿直線l：y=x-2平移m個單位長度，若直線AB平分矩形C′O'D'E'的面積，請直接寫出此時點E'的坐標．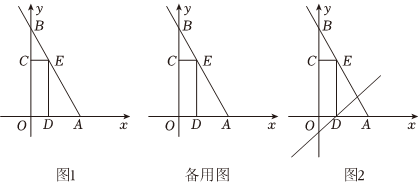
組卷：338引用：1難度：0.2
解析
22．小明在學習《圖形的平移與旋轉》時，認識了“手拉手模型”，并發現它在中考中重要應用，請你與小明一起完成下面練習．
【問題呈現】
2021年北京中考：如圖1，在△ABC中，AB=AC，∠BAC=α，點D在線段BC上，以點A為中心，將線段AD順時針旋轉α得到線段AE，連接BE，DE．
【模型分析】
（1）如圖1，小明通過審題發現△ABC和△AED為共頂點A的等腰三角形，這是老師經常提及的“手拉手模型”，由∠BAC=∠EAD=α可得∠EAB=∠DAC，因為AB=AC，AD=AE可證明：△AEB≌△ADC，利用角的等量關系進一步推導出：∠EBC=
．（用含α的式子表示）
【模型應用】
小明發現利用“手拉手模型”可將題目中分散的條件集中到某一處，從而快速找到解決問題的線索．
（2）如圖2，在平面直角坐標系中，點A（0，2）在y軸上，以OA為邊向右側作等邊△OAB，點D為x軸正半軸的動點，以AD為邊向右側作等邊△ADE，直線EB交y軸于點F．當點D在x軸的正半軸運動時，點F的坐標是否變化，若不變，請求出點F的坐標，若變化，請說明理由．
【模型拓展】
小明發現“手拉手模型”常常“隱藏”在有一個內角是60°的菱形中，可以連接菱形的其中一條對角線，將它分成兩個全等的等邊三角形．
（3）2018年江西中考：如圖3，在菱形ABCD中，∠ABC=60°，點P在線段BD的延長線上，以AP為邊向右側作等邊△APE，連接BE，若
AB
=
2
3
，
BE
=
2
19
，求四邊形ADPE的面積．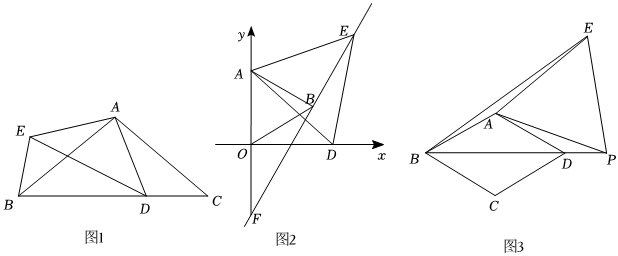
??
組卷：1059引用：1難度：0.1
解析