2022-2023學年江蘇省無錫一中高二（下）期中數學試卷
發布：2024/8/3 8:0:9
一.單項選擇題：本題共8小題，每小題5分，共40分，在每小題給出的四個選項中，只有一項是符合題目要求的.
-
1．若
，則m=（ ）A2m=6Cm-2m-1組卷：201引用：1難度：0.8 -
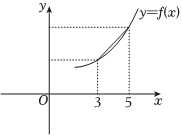2．y=f（x）的圖象如圖所示，f′（x）是函數f（x）的導函數，則下列排序正確的是（ ）組卷：157引用：6難度：0.8 -
3．已知隨機變量X的分布列如表，則E（5X-1）=（ ）
X 0 2 4 P 0.3 a 0.5 組卷：169引用：1難度：0.9 -
4．已知a=ln2.68，b=4.5×0.62，c=1.15，則下列排序正確的是（ ）
組卷：35引用：1難度：0.6 -
5．當x∈（0，+∞）時，函數f（x）=xlnx的圖象恒在函數g（x）=-x2+3x+a圖象的上方，則a的取值范圍是（ ）
組卷：154引用：1難度：0.6 -
6．若a,b∈{1，2，3}，則在“函數f（x）=ln（x2+ax+b）的定義域為R”的條件下，“函數g（x）=ax-b-x為奇函數”的概率為（ ）
組卷：82引用：5難度：0.6 -
7．已知f′（x）為函數f（x）的導函數，且f′（x）+lnx＞-1，f（e）=1，則不等式f（x）+xlnx＜e+1的解集為（ ）
組卷：164引用：1難度：0.6
四.解答題：本題共6小題、17題10分，其余每小題10分共70分，解答應寫出文字說明、證明過程或漬算步驟.
-
21．在社會學調查中經常會遇到調查敏感性問題的情形，如在無錫市范圍內調查高中二年級學生默寫作弊情況時，直接調查往往難以得到真實的結果．運用西蒙斯模型（simmons-model）可以有效提高數據的可靠性．首先準備含有m個大小、形狀相同的球，其中n個紅球，其余為白球，對調查對象準備兩個問題，分別為：
問題1：你的出生月份為奇數嗎？（回答是、否）
問題2：你在默寫過程中有作弊行為嗎？（回答是、否）
被調查者在填寫問卷時，先從箱中摸出一個球，如果是紅球則回答問題1，是白球則回答問題2．
記回答問題1為事件A1，回答問題2為事件A2，問卷結果為“是”為事件B．在工作人員回避的情況下，我們可以利用全概率公式估算問題2回答為“是”的概率．
（1）若m=25，n=10，回收調查問卷100份，其中回答為“是”的30份．求P（B|A1），并估算本次調查群體的默寫作弊概率P（B|A2）．
（2）利用數學工具可以估計：在回答“是”的被調查者中，所答問題為“問題 2“的概率P（A2|B）．
①試證明；P（A2|B）=P（B|A2）P（A2）P（B|A1）P（A1）+P（B|A2）P（A2）
②在（1）的情況下，估算P（A2|B）．組卷：90引用：1難度：0.5 -
22．已知函數f（x）=lnx+a,設A（x1，f（x1）），B（x2，f（x2）），且x1≠x2．
（1）若a=-1，求函數y=f（x）在P（1，f（1））處的切線方程；
（2）證明：．f（x2）-f（x1）x2-x1＞f′（x1+x22）組卷：153引用：3難度：0.5