2021-2022學年浙江省麗水市高二（下）期末數(shù)學試卷

一、單項選擇題：本大題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的。

• 1．已知集合A={-1，0，1，2}，B={0，1，2，3}，則A∩B=（　　）

  A．{-1，0，1，2，3}

  B．{0，1，2，3}

  C．{0，1，2}

  D．{-1，0，1，2}
  組卷：66引用：1難度：0.9

  解析

• 2．已知向量

  a

  =（3，0），

  b

  =（1，1），且（

  a

  -2

  b

  ）∥（2

  a

  +k

  b

  ），則實數(shù)k的值是（　　）

  A．2

  B．-2

  C．4

  D．-4
  組卷：130引用：2難度：0.7

  解析

• 3．已知a∈R，則“a＞1”是“

  1

  a

  ＜1”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充要條件	D．既不充分也不必要條件
  組卷：1109引用：68難度：0.8

  解析

• 4．已知角α的終邊經過點P（-1，m），且sinα=-

  3

  5

  ，則tanα的值是（　　）

  A． ± 3 4

  B． 3 4

  C．- 3 4

  D． 4 3
  組卷：389引用：3難度：0.7

  解析

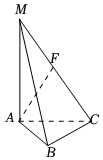• 5．如圖，在三棱錐M-ABC中，MA⊥平面ABC，△ABC是邊長為2的正三角形，MA=2

  3

  ，F(xiàn)是MC的中點，則異面直線MB與AF所成角的余弦值是（　　）

  A． 3 3

  B． 3 4

  C． 13 3

  D． 5 8
  組卷：140引用：8難度：0.7

  解析

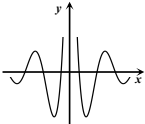• 6．函數(shù)y=f（x）的部分圖象如圖所示，則函數(shù)y=f（x）的解析式可能是（　　）

  A．f（x）= sin 6 x 2 - x - 2 x	B．f（x）= cos 6 x 2 x - 2 - x
  C．f（x）= cos 6 x | 2 x - 2 - x |	D．f（x）= sin 6 x | 2 x - 2 - x |
  組卷：64引用：1難度：0.7

  解析

• 7．已知△ABC的內角A，B，C的對邊分別為a,b,c,則下列命題中正確的是（　　）

  A．若acosA=bcosB，則△ABC為等腰三角形

  B．若A=30°，a=3，b=4，則△ABC有唯一解

  C．若△ABC為銳角三角形，則sinA+sinB＞cosA+cosB

  D．若A=60°，a=2，則△ABC面積的最大值為2 3
  組卷：156引用：3難度：0.6

  解析

四、解答題：本題共6小題，共70分解答應寫出文字說明、證明過程或演算步驟.。

• 21．已知函數(shù)f（x）=x²-4x+a（x∈R）．
  （1）若x∈（1，3）時，不等式log₂f（x）≤1恒成立，求實數(shù)a的取值范圍；
  （2）若關于x的方程f（2^x+1）+（a+2）|2^x-1|+8=0有三個不同的實數(shù)解，求實數(shù)a的取值范圍．
  組卷：205引用：3難度：0.3

  解析

• 22．已知函數(shù)f（x）=2x+

  a

  x

  ，g（x）=x|x-a|-2x+4（a＞0）．
  （1）當a=1時，求g（x）的單調區(qū)間；
  （2）對任意的x₀∈[1，2]，總存在x₁，x₂，x₃∈R（x₁，x₂，x₃互不相等），使得f（x₀）=g（x_i）（i=1，2，3），求實數(shù)a的取值范圍．
  組卷：36引用：1難度：0.5

  解析