2023-2024學年遼寧省沈陽市東北育才學校科學高中部高一（上）第一次月考數學試卷

一、選擇題：本題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的．

• 1．命題“?x＞0，-x²+2x-1＞0”的否定為（　　）

  A．?x＞0，-x2+2x-1≤0	B．?x≤0，-x2+2x-1＞0
  C．?x＞0，-x2+2x-1≤0	D．?x≤0，-x2+2x-1＞0
  組卷：322引用：6難度：0.5

  解析

• 2．已知集合A={x|x²-5x+4≥0}，集合B={x∈Z||x-1|≤2}，則集合（?_RA）∩B的元素個數為（　　）

  A．1

  B．2

  C．3

  D．4
  組卷：122引用：3難度：0.7

  解析

• 3．已知x,y∈R，則“x+y≤1”是“x

  ≤

  1

  2

  或y

  ≤

  1

  2

  ”的（　　）

  A．充分且不必要條件	B．必要且不充分條件
  C．充分且必要條件	D．不充分也不必要條件
  組卷：440引用：6難度：0.5

  解析

• 4．已知實數x,y滿足-4≤x-y≤-1，-1≤4x-y≤5，則z=9x-y的取值范圍是（　　）

  A．{z|-7≤z≤26}

  B．{z|-1≤z≤20}

  C．{z|4≤z≤15}

  D．{z|1≤z≤15}
  組卷：264引用：13難度：0.6

  解析

• 5．設集合A，B，C均為非空集合．（　　）

  A．若A∩B=B∩C，則A=C	B．若A∪B=B∪C，則A=C
  C．若A∩B=B∪C，則C?B	D．若A∪B=B∩C，則C?B
  組卷：408引用：6難度：0.9

  解析

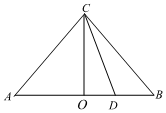• 6．數學里有一種證明方法叫做Proofswithoutwords,也稱之為無字證明，一般是指僅用圖象語言而無需文字解釋就能不證自明的數學命題，由于這種證明方法的特殊性，無字證明被認為比嚴格的數學證明更為優雅．現有如圖所示圖形，在等腰直角三角形ABC中，點O為斜邊AB的中點，點D為斜邊AB上異于頂點的一個動點，設AD=a,BD=b,則該圖形可以完成的無字證明為（　　）

  A． a + b 2 ≥ ab （ a ＞ 0 ， b ＞ 0 ）	B． a + b 2 ≤ a 2 + b 2 2 （ a ＞ 0 ， b ＞ 0 ）
  C． 2 ab a + b ≤ ab （ a ＞ 0 ， b ＞ 0 ）	D． a 2 + b 2 ≥ 2 ab （ a ＞ 0 ， b ＞ 0 ）
  組卷：559引用：8難度：0.5

  解析

• 7．用C（A）表示非空集合A中的元素個數，定義

  A

  *

  B

  =

  C （ A ） - C （ B ） ， C （ A ） ≥ C （ B ）

  C （ B ） - C （ A ） ， C （ A ） ＜ C （ B ）

  ，若A={1，2}，B={x|（x²+ax）?（x²+ax+2）=0}，且A*B=1，設實數a的所有可能取值組成的集合是S，則C（S）等于（　　）

  A．1

  B．3

  C．5

  D．7
  組卷：1135引用：6難度：0.5

  解析

四、解答題：本題共6小題，共70分．解答應寫出文字說明、證明過程或演算步驟．

• 21．某學校要建造一個長方體形的體育館，其地面面積為240m²，體育館高5m,如果甲工程隊報價為：館頂每平方米的造價為100元，體育館前后兩側墻壁平均造價為每平方米150元，左右兩側墻壁平均造價為每平方米250元，設體育館前墻長為x米．
  （1）當前墻的長度為多少時，甲工程隊報價最低？
  （2）現有乙工程隊也參與該校的體育館建造競標，其給出的整體報價為

  12000

  +

  500

  （

  a

  +

  1152

  x

  +

  a

  ）

  元（a＞0），若無論前墻的長度為多少米，乙工程隊都能競標成功，試求a的取值范圍．
  組卷：112引用：16難度：0.4

  解析

• 22．問題：正數a,b滿足a+b=1，求

  1

  a

  +

  2

  b

  的最小值．其中一種解法是：

  1

  a

  +

  2

  b

  =

  （

  1

  a

  +

  2

  b

  ）

  （

  a

  +

  b

  ）

  =

  1

  +

  b

  a

  +

  2

  a

  b

  +

  2

  ≥

  3

  +

  2

  2

  ，當且僅當

  b

  a

  =

  2

  a

  b

  ，且a+b=1時，即a=

  2

  -1且b=2-

  2

  時取等號，學習上述解法并解決下列問題：
  （1）若正實數x,y滿足xy=3x+y,求x+y的最小值；
  （2）若正實數a,b,x,y滿足

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =1，且a＞b,試比較a²-b²和（x-y）²的大小，并說明理由；
  （3）若m＞0，利用（2）的結論，求代數式M=

  3

  m

  -

  5

  -

  m

  -

  2

  的最小值，并求出使得M最小的m的值．
  組卷：280引用：12難度：0.6

  解析