2014年浙江省杭州四中保送生入學考試數學試卷

一、仔細選一選（本題有6個小題，每小題5分，共30分）

• 1．下列說法中
  ①一個角的兩邊分別垂直于另一角的兩邊，則這兩個角相等
  ②數據5，2，7，1，2，4的中位數是3，眾數是2
  ③若點A在y=2x-3上，且點A到兩坐標軸的距離相等時，則點A在第一象限；
  ④半徑為5的圓中，弦AB=8，則圓周上到直線AB的距離為2的點共有四個．
  正確命題有（　　）

  A．0個

  B．1個

  C．2個

  D．3個
  組卷：90引用：2難度：0.9

  解析

• 2．在y=□2x²□8x□8的“□”中，任意填上“+”或“-”，可組成若干個不同的二次函數，其中其圖象的頂點在x軸上的概率為（　　）

  A． 1 4

  B． 1 3

  C． 1 2

  D．1
  組卷：302引用：9難度：0.9

  解析

• 3．若實數a,b滿足ab=1，設M=

  a

  a

  +

  1

  +

  b

  b

  +

  1

  ，N=

  1

  a

  +

  1

  +

  1

  b

  +

  1

  ，則M，N的大小關系是（　　）

  A．M＞N

  B．M=N

  C．M＜N

  D．不確定
  組卷：3582引用：38難度：0.5

  解析

• 4．如圖，A、B是雙曲線

  y

  =

  k

  x

  （

  k

  ＞

  0

  ）

  上的點，A、B兩點的橫坐標分別是a、2a,線段AB的延長線交x軸于點C，若S_△AOC=6．則k的值為（　　）

  A．1

  B．2

  C．4

  D．無法確定
  組卷：1204引用：6難度：0.9

  解析

• 5．二次函數y=x²-x+m（m為常數）的圖象如圖所示，當x=a時，y＜0；那么當x=a-1時，函數值（　　）

  A．y＜0

  B．0＜y＜m

  C．y＞m

  D．y=m
  組卷：8758引用：52難度：0.5

  解析

二、解答題（本大題有4個小題，共45分）

• 14．在研究問題“已知

  3 a + 7 b + c = 4

  a - b - 3 c = 8

  ，求a+b-c的值．”時，三個同學各提出了自己的看法．甲說：“三個未知數，兩個方程，條件不夠，不能求出abc的值，a+b-c的值很難確定．”；乙說：“是求a+b-c的值，可以把a+b-c看作一個整體，設a+b-c=m,應該可以求解”；丙說：“可以把其中一個未知數c當做已知量，三元一次方程組化為二元一次方程組，從而求出a,b的表達式，再求a+b-c的值”．
  （1）根據他們的說法，請用合適的方法求a+b-c的值；
  （2）若已知b≤c,你能確定c²+a-2b是否有最值？若有，請求出最值和相應的a、b、c的值．
  組卷：161引用：1難度：0.3

  解析

• 15．如圖，在梯形AOBC中，AC∥OB，AO⊥OB，OA=4，OB=10，tan∠OBC是方程x²+

  3

  2

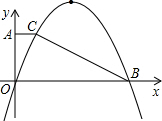  x-1=0的一個根，以O為坐標原點，OB、OA所在的直線分別為x軸，y軸建立平面直角坐標系．
  （1）求C點坐標；
  （2）求經過O、C、B三點的拋物線解析式；
  （3）M是（2）中拋物線上一動點，過M作x軸的平行線交（2）中的拋物線于另一點N（M在N左側）．問：是否存在點M使得以MN為直徑的圓正好與x軸相切？若不存在，請說明理由；若存在，求此圓的半徑．
  組卷：217引用：3難度：0.5

  解析