2023-2024學年江蘇省無錫市梁溪區積余實驗學校九年級（上）期中數學試卷
發布：2024/10/9 9:0:1
一、選擇題（本大題共10小題，每小題3分，共30分）
-
1．下列方程是一元二次方程的是（ ）
組卷：236引用：3難度：0.8 -
2．一元二次方程x2+x+1=0的根的情況是（ ）
組卷：72引用：6難度：0.7 -
3．如果一個一元二次方程的根是x1=x2=-3，那么這個方程可以是（ ）
組卷：19引用：1難度：0.7 -
4．電影《雄兵出擊》以朝鮮戰爭爆發為背景，講述了中國志愿軍官兵在炮火硝煙中入朝作戰的歷程，展現了中國人民志愿軍的愛國主義精神和革命英雄主義精神，一上映就獲得全國人民的追捧，第一天票房約2億元，以后每天票房按相同的增長率增長，第三天票房為5億元，方程可以列為（ ）
組卷：235引用：4難度：0.5 -
5．已知點P與⊙O在同一平面內，⊙O的半徑為4，點P到圓心O的距離是5，則點P與⊙O的位置關系是（ ）
組卷：13引用：1難度：0.7 -
6．下列說法中正確的命題是（ ）
組卷：25引用：1難度：0.7 -
7．如圖，AB是⊙O的直徑，弦CD⊥AB于點M，若CD=AM=8cm,則直徑AB的長為（ ）組卷：38引用：1難度：0.5 -
8．如圖，四邊形ABCD是⊙O的內接四邊形，∠ABC=125°，則∠AOC 的度數是（ ）組卷：234引用：6難度：0.9 -
9．如圖，半圓O的直徑AB=8，弦CD=4，弦CD在半圓上滑動，點C從點A開始滑動，到點D與點B重合時停止滑動，若M是CD的中點，則在整個滑動過程中線段BM掃過的面積為（ ）2組卷：168引用：1難度：0.4
三、解答題：（本大題共9小題，共96分）
-
26．（1）【學習心得】
小宸同學在學習完“圓”這一章內容后，感覺到一些幾何問題，如果添加輔助圓，運用圓的知識解決，可以使問題變得非常容易．
例如：如圖1，在△ABC中，∠BAC=90°，AB=AC=AD，求∠BDC 的度數，若以點A為圓心，AB為半徑作輔助圓⊙A，則點C、D必在⊙A上，∠BAC是⊙A的圓心角，而∠BDC是圓周角，從而可容易得到∠BDC=°．
（2）【問題解決】
如圖2，在四邊形ABCD中，∠BAD=∠BCD=90°，∠BAC=26°，求∠BDC 的度數．小宸同學認為用添加輔助圓的方法，可以使問題快速解決，他是這樣思考的：△ABD 的外接圓就是以BD的中點為圓心，BD長為半徑的圓；△BCD的外接圓也是以BD的中點為圓心，12BD長為半徑的圓．這樣A、B、C、D四點在同一個圓上，進而可以利用圓周角的性質求出∠BDC 的度數，請運用小底的思路解決這個問題．12
（3）【問題拓展】
①如圖3，△ABC的三條高AD、BE、CF相交于點H，求證：∠EFC=∠DFC．
②如圖4，在△ABC中，∠BAC=45°，AD是BC邊上的高，且BD=3，CD=1，直接寫出AD的長．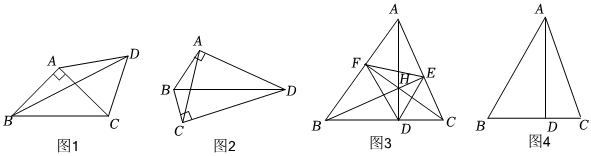
組卷：1191引用：7難度：0.1 -
27．在△ABC中，∠A=90°，AB=AC，給出如下定義：作直線l分別交AB、AC邊于點M、N，點A關于直線l 的對稱點為A，則稱A′為等腰直角△ABC 關于直線l的“直角對稱點”．（點M可與點B重合，點N可與點C重合）
（1）在平面直角坐標系xOy 中，點A（0，4）、B（-4，0），直線ky=kx+2，O'為等腰直角△AOB 關于直線l的“直角對稱點”．
①當k=1時，寫出點O'的坐標 ；
②連接BO，求BO 長度的取值范圍；
（2）⊙O的半徑為8，點M是⊙O上一點，以點M為直角頂點作等腰直角△MPQ，其中MP=1，直線l與MP、MQ分別交于E、F兩點，同時 M'為等腰直角△MPQ關于直線的“直角對稱點”，連接OM；當點M在⊙O上運動時，直接寫出OM'長度的最大值與最小值．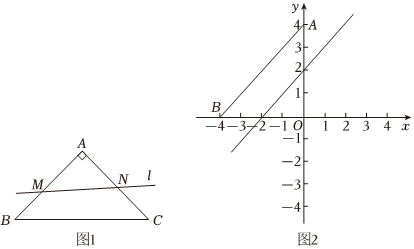
組卷：97引用：1難度：0.1